Proportions are nice to work with when you're solving rational equations, because you can eliminate the fractions or change them so that they feature better denominators.
A proportion is an equation in which one fraction is set equal to another. For example, the equation
is a proportion.
When you have the proportion
the following are also true:
the cross-products, ad and bc, are equal, giving you ad = bc.
the reciprocals,

are equal (you can flip the proportion).
Another wonderful feature of proportions is that you can reduce the fractions in a proportion by finding common factors in four different directions: top, bottom, left, and right. The ability to reduce a proportion comes in handy when you have large numbers in the equation.
Here are the rules for reducing proportions across the top (numerators), bottom (denominators), left, and right, and an example for each:

The reduced forms of the proportions make cross-multiplication much easier and more manageable. Take the following proportion, for example. You first reduce across the numerators, and then you reduce the left fractions.
reduces
which reduces again
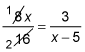
which is then written
Now cross multiply and solve the quadratic equation.
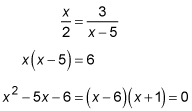
When x – 6 = 0, x = 6; and when x + 1 = 0, x = –1. Both solutions check out.
To solve an equation such as
you can find a common denominator and then multiply each side by the common denominator, but here's a quicker, easier way:
Add

to each side and add the terms with the same denominator to form a proportion.

Cross multiply.
(x + 5)x = 24
Simplify the quadratic equation, and set it equal to zero.
x2 + 5x = 24 becomes x2 + 5x – 24 = 0
Solve for the solutions by factoring.
(x + 8)(x – 3) = 0
The solutions are x = –8 or x = 3. Both work.





