The TI-Nspire Geometry application offers Lock and Pin features. If a point is pinned, it can’t be moved unless it is unpinned. Other geometric objects and text can also be pinned, which is a nice feature, because it prevents someone from accidentally moving the wrong point or grabbing and moving a label instead of a point.
Insert a new Geometry page (press [CTRL][I] and choose Add Geometry). Now draw a triangle with a horizontal base (press [MENU]→Shapes→Triangle (don’t forget to hold the [SHIFT] key down to construct a horizontal line).Then follow these steps to construct an ellipse:
Secure the two vertices of the triangle for the side that is horizontal, which will become the foci of the ellipse. Move your cursor over the vertex, right-click ([CTRL][MENU]), and choose Pin.
See the first screen.
Repeat Step 1 for the second vertex.
Measure the perimeter of the triangle. Press [MENU]→Measurement→Length. Move your cursor over the triangle until
appears, then [CLICK] twice to anchor the measurement.
When finding the perimeter of a polygon, notice that the word describing the polygon (triangle, rectangle, or polygon) appears along with the e symbol. Press [TAB] to switch to finding the length of the side of the polygon corresponding to the current cursor location. Press [TAB] again to switch back to finding the perimeter of the polygon.
Move your cursor over the perimeter measurement, right-click, [CTRL][MENU]->Attributes, and use your Touchpad to lock the measurement.
See the second screen.
Press [MENU]→Trace→Geometry Trace.
Move your cursor over the third vertex of the triangle, click the vertex to indicate that you want the geometry trace of that point, grab the point ([CTRL][CLICK]), and then use the Touchpad to move it around to form the ellipse.
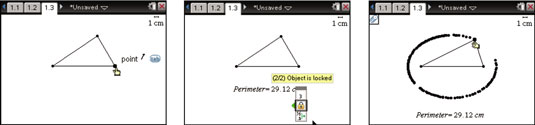
The third screen shows a nifty mathematical reason for locking the perimeter of a triangle. By using Geometry Trace, you can trace the path of the vertex of a triangle with a fixed perimeter. The tracing results in an ellipse because the sum of the lengths of the two sides of the triangle that meet this vertex must be constant. How cool is that?
You may also want to try locking the perimeter of a rectangle, which can facilitate finding the maximum area for a fixed perimeter.

