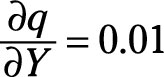In most instances, two variable functions are too simplistic to describe a situation adequately when it comes to using calculus in managerial economics. When functions have three or more variables (two or more independent variables), economists frequently want to focus on how changes in one independent variable’s value affect the dependent variable’s value.
Consider a situation where the quantity sold of your firm’s product depends on the product’s price, p, consumer incomes, Y, and the amount of money spent on advertising, A, or
You may be primarily interested in how your advertising affects the quantity sold.
In order to determine this relationship, you want to determine the incremental or marginal effect that advertising has on quantity, q, while holding everything else — the other independent variables — constant.
Obtain this information by taking the partial derivative of the function with respect to advertising.
You obtain a partial derivative by applying the rules for finding a derivative, while treating all independent variables, except the one of interest, as constants. Thus, in the example, you hold constant both price and income. And the great thing about constants is their derivative equals zero!
Assume the following equation describes the relationship between the quantity sold of a good and its price, consumer incomes, and the amount spent on advertising
where q is the number of units sold per month, p is the price per unit in dollars, Y is average consumer income in dollars, and A is advertising expenditures in dollars.
In order to determine the partial derivative of quantity with respect to advertising, you should take the following steps:
First, remember that both p and Y are treated as constants. Therefore, you treat them exactly as you would a number when taking the derivative.
To take the partial derivative of q with respect to A, start with the first term “1,000” and its derivative equals zero in the partial derivative.
The second term “–10p” has a partial derivative equal to zero because you treat the p like a constant or number.
The next term “+0.01Y” also has a partial derivative equal to zero because you treat the Y like a constant.
The derivative of the term “0.2A” equals 0.2, because you treat the A like a variable in this partial derivative. You’re interested in determining how changes in A’s value affect q.
The derivative of the term “–0.01A×p” equals –0.01p. Remember, you treat p the same as any number, while A is the variable.
Finally, derivative of the term “–0.0001A2” equals –0.0002A.
Putting each of these steps together yields a partial derivative of q with respect to A of
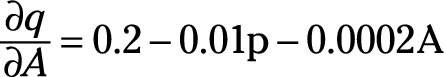
Similarly, the partial derivative of quantity with respect to price, δq/δp, and the partial derivative of q with respect to Y, δq/δY, can be determined by treating any variables other than those specified in the partial derivative as constants. Those partial derivatives would be
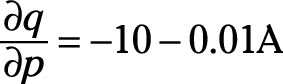
and