Fortunately, your TI-84 Plus calculator knows how to handle complex numbers. Complex numbers are of the form a + bi, where a is the real part and b is the imaginary part.
Early on in your math journey, you were probably told that you can’t take the square root of a negative number. Then a teacher blew your mind by saying you really can take the square root of a negative number and the result will contain the imaginary number, i.
Setting the mode for complex numbers
Try evaluating the square root of –1 in your calculator. On the Home screen, press [2nd][x2][(-)][1][ENTER].There’s a good chance you’ll get an ERROR: NONREAL ANSWERS message, as shown in the first screen.
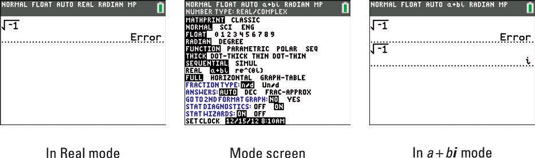
In Real mode, your calculator usually returns an error for a complex-number result. The exception is when you enter your expression using i. In this case, your calculator produces a complex-number result regardless of the mode. The good news is you can avoid this error altogether by setting the mode of your calculator to a + bi.
To set the mode to a + bi, follow these steps:
Press [MODE] to access the mode screen.
Press the down-arrow key repeatedly to navigate to the eighth row.
Press the right-arrow key to highlight a + bi.
Press [ENTER] to change the mode (see the second screen).
Now, try evaluating the square root of –1 a second time in your calculator.
Press the up-arrow key to scroll through your previous calculations. When a previous entry or answer is highlighted, press e to paste into your current entry line.
Success! See the result on the third screen.
Entering complex numbers on the TI-84 Plus
You can enter an expression that includes the imaginary number, i, by pressing [2nd][.]. Somewhere along the way, you have probably learned that i2 = –1. Interestingly enough, your calculator not only knows that i2 = –1, but automatically simplifies any result that would have had i2 in it.
For example, multiplying (2 + i)(2 + i) would yield the trinomial, 4 + 4i + i2. Of course, this answer can be simplified to 3 + 4i. Your calculator only shows the simplified answer, as shown in the first screen.
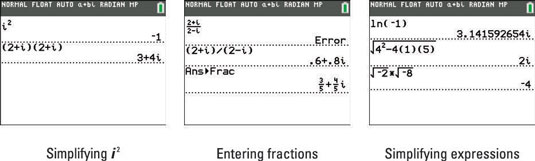
Complex numbers may not be used with the n/d fraction template. Instead, enter complex numbers as fractions using parentheses and the division key. Press [MATH][ENTER][ENTER] to display the complex number answer in fraction form. See the second screen.
In a + bi mode, you can take the logarithm or square roots of negative numbers! Often, using your calculator protects you from making mistakes that are all too common for students. For example, given the expression,
many students will mistakenly think the answer is 4. Before applying the order of operations, always simplify the negative inside of a square root! Here is the mathematical progression that your calculator used to simplify the given expression,
Pretty cool, huh?
Interpreting strange-looking results for complex number calculations
A common classroom math activity is to explore the powers of the imaginary number, i. Mathematics is about finding patterns, and there’s an interesting pattern that emerges when you explore the powers of i. The results of the first four powers of i form a repeating pattern as i is raised to successive higher powers. See the first screen.
Using your calculator, something unexpected happens when you evaluate i7. You might expect the answer, –i. Instead, the calculator displayed –3E–13–i, as shown in the second screen.
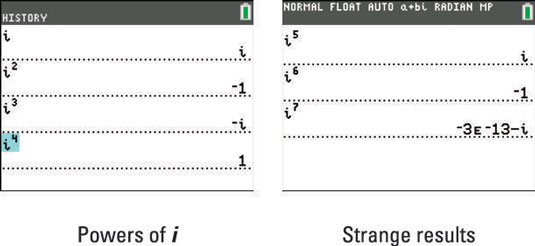
To decipher this strange result, you must first remember that complex numbers are written in the form a + bi. Using parentheses to separate the real and imaginary parts, the calculated result looks like this, (–3E–13) – (i). Now, remember that –3E–13 is equal to –3*10–13 in scientific notation. This is an extremely small number!
What can you learn from this strange result? You should be wary of calculated results that are extremely small! It’s likely that your calculator should have returned a result of zero. The reality is that your calculator deals with approximate results all the time. You usually don’t notice this because the calculator regularly comes up with the results that you expect.





