The study of signals and systems establishes a mathematical formalism for analyzing, modeling, and simulating electrical systems in the time, frequency, and s- or z-domains. Signals exist naturally and are also created by people. Some operate continuously (known as continuous-time signals); others are active at specific instants of time (and are called discrete-time signals).
Signals pass through systems to be modified or enhanced in some way. Systems that operate on signals are also categorized as continuous- or discrete-time.
Mathematics plays a central role in all facets of signals and systems. Specifically, complex arithmetic, trigonometry, and geometry are mainstays of this dynamic and (ahem) electrifying field of work and study. This article highlights the most applicable concepts from each of these areas of math for signals and systems work.
Complex arithmetic for signals and systems
Here are some of the most important complex arithmetic operations and formulas that relate to signals and systems.

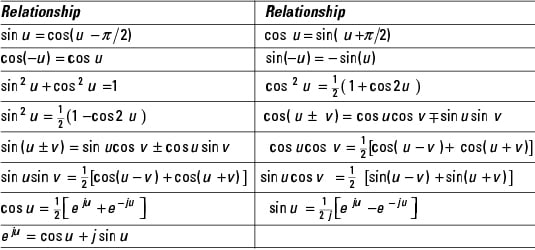
Trigonometry and Euler's formulas
This table presents the key formulas of trigonometry that apply to signals and systems:
Geometric series
Among the most important geometry equations to know for signals and systems are these three:


