How to Determine the Advertising Elasticity of Demand in Managerial Economics

The advertising elasticity of demand measures the responsiveness of a good’s demand to changes in spending on advertising. The advertising elasticity of demand measures the percentage change in demand that occurs given a 1 percent change in advertising expenditure.

The advertising elasticity of demand is calculated using the following formula:

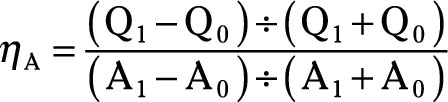
The symbol η_A represents the advertising elasticity of demand. In the formula, the symbol Q₀ represents the initial demand or quantity purchased that exists when spending on advertising equals A₀. The symbol Q₁ represents the new demand that exists when advertising expenditures change to A₁.

The advertising elasticity of demand should be positive. (A negative value would indicate the more you spend on advertising, the lower your sales. That is a really bad ad! You should probably fire whomever is in charge of advertising.)

As with all elasticity values, the larger the number, the more responsive the good’s demand is to a change in advertising.

Your vending machine company starts a new ad campaign, “Vend for Yourself.” Currently, your company sells soft drinks at $1.50 per bottle, and at that price, customers purchase 2,000 bottles per week. Initially, you spend $400 per week on advertising. After a month, you’re spending $500 per week on advertising and, without changing the price of soft drinks, sales have increased to 3,000 bottles per week.

The advertising elasticity of demand tells you how responsive your vending machine soft drink sales are to the change in advertising expenditures.

To determine the advertising elasticity of demand, follow the customary steps:

1. Because $400 and 2,000 are the initial advertising expenditures and quantity sold, put $400 into A₀ and 2,000 into Q₀.

2. Because $500 and 3,000 are the new spending on advertising and sales, put $500 into A₁ and 3,000 into Q₁.

3. Divide the expression on top of the equation.

   (Q₁ – Q₀) equals 1,000 and (Q₁ + Q₀) equals 5,000. Dividing 1,000 by 5,000 equals 1/5.

4. Divide the expression in the bottom of the equation.

   (A₁ – A₀) equals $100, and (A₁ + A₀) equals $900. Dividing $100 by $900 equals 1/9.

5. Divide the top result, 1/5, by the bottom result, 1/9.

   You get the advertising elasticity of demand equal to 9/5 or 1.8. Thus, the advertising elasticity of demand for soft drinks equals

   

You can conclude that a 1 percent increase in advertising expenditures increases demand 1.8 percent.