We know that business managers do not always make the most profitable economic choices. Otherwise, there wouldn’t be so many failures. Managerial economics uses game theory to help to explain this observation. For instance, a prisoner’s dilemma in game theory refers to a game in which players individually choose something less than the optimal combined actions.
The illustration presents the payoff table of monthly profits for two competing restaurants — Bob’s Barbecue and Clara’s Cafeteria. Both Bob and Clara are deciding whether or not to expand their menus, and the resulting payoff depends upon not only the decision each of them makes but also on the decision their rival makes.
In determining the ultimate payoff, you should first identify whether or not either restaurant has a dominant action. To identify any dominant actions and determine the ultimate payoff, you take the following steps:
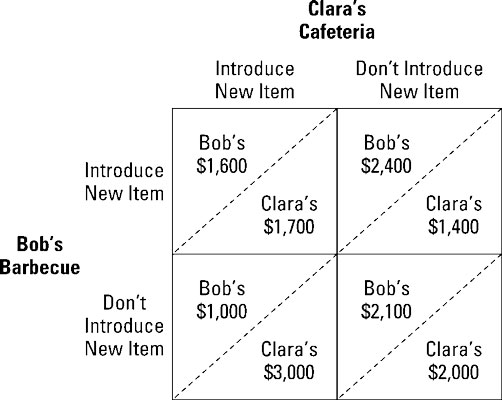
Determine how Clara responds to Bob’s decisions.
If Bob introduces a new menu item, Clara should also introduce a new menu item because her monthly profit is $1,700 instead of $1,400. If Bob doesn’t introduce a new menu item, Clara should introduce a new menu item because her monthly profit is $3,000 instead of $2,000.
Introducing a new menu item is a dominant action for Clara because its payoff is always higher than not introducing a new menu item.
Determine how Bob responds to Clara’s decisions.
If Clara introduces a new menu item, Bob should also introduce a new menu item because his monthly profit is $1,600 instead of $1,000. If Clara doesn’t introduce a new menu item, Bob should introduce a new menu item because his monthly profit is $2,400 instead of $2,100.
Introducing a new menu item is a dominant action for Bob because its payoff is always higher than not introducing a new menu item.
Determine the ultimate payoff.
Because introducing a new menu item is the dominant action for both Bob and Clara, the ultimate payoff is in the upper left cell of the payoff table. Bob’s Barbecue receives $1,600 profit and Clara’s Cafeteria receives $1,700 profit.
This example leads to a prisoner’s dilemma because Bob and Clara ultimately receive profits that are less than optimal. If both Bob and Clara decide not to introduce a new menu item, both receive more profit — $2,100 for Bob and $2,000 for Clara. But Bob and Clara don’t do that, because in that situation, each could make more profit by introducing a new menu item.
If Bob introduces a new menu item, his profit goes to $2,400, but Clara’s profit goes down to $1,400. So, Clara is “forced” to also introduce a new menu item to get her profit from $1,400 to $1,700, but Bob’s profit goes down to $1,600.
Similarly, if Clara introduces a new menu item, her profit goes to $3,000, but Bob’s profit goes down to $1,000. So, Bob is “forced” to also introduce a new menu item to get his profit from $1,000 to $1,600, but then Clara’s profit goes down to $1,700. By acting out of self interest, both Bob and Clara end up with smaller profit, but ignoring their rival’s actions is even worse.
With a prisoner’s dilemma, players chose the action that best serves their own interests. However, the result of this behavior is a combined payoff that’s less than optimal.





