Companies usually have limited resources, such as limits on space, on the number of workers, or even on the machine capacity needed to produce goods. This reality means that in order to best use limited production capabilities, managers must choose which products to make and sell.
Managerial accountants use a simple technique of dividing contribution margin by a measure of the constrained resource to indicate which products squeeze the most profitability out of constrained resources.
Suppose Charlie’s Burger Restaurant is constrained by the size of its 1,000-square-inch cooking grill. Because the restaurant is open eight hours a day, Charlie’s has a maximum of 8,000 square-inch-hours of grill time available per day (1,000 square inches times eight hours). To keep things simple, call these units of grill time.
Suppose that one medium-cooked Deluxe Burger requires eight units of grill time. Charlie’s maximum capacity of medium-cooked burgers, therefore, equals the total capacity of 8,000 units of grill time divided by the 8 units needed for each burger. Therefore, in theory at least, Charlie’s can produce a maximum of 1,000 medium-cooked Deluxe Burgers a day.
As long as Charlie’s customers demand fewer than 1,000 Deluxe Burgers a day, capacity is no problem. Charlie’s cook can make as many burgers as customers order.
However, when a company doesn’t have enough capacity to meet its needs, it must carefully consider the best way to use its constrained resource. Here, if Charlie’s customers demand more than 1,000 burgers a day (or, for that matter, more food at any one time than can fit on the cooking grill during that time span), managers must decide how to allocate the restaurant’s limited cooking space.
Given that your business has to deal with at least one constraint that limits your ability to make and sell the products your customers want, how can you adjust your sales to make the best possible use of the constraint? Apply this technique: Divide contribution margin by a measure of the constrained resource to determine which products squeeze the most profitability out of constrained resources.
Following this technique helps you choose which products deliver the most profitability.
Say that Charlie’s Burger Restaurant has four total items on the menu, with the following contribution margins and grill time requirements per order:
| Item | Contribution Margin | Grill Time |
|---|---|---|
| Deluxe Burger | $4.50 | 8 units |
| Juicy Grilled Chicken | $4.00 | 12 units |
| Puffy Hot Dog | $2.00 | 3 units |
| Vegetarian Pasta Primavera | $6.00 | 0 units |
First, find each product’s contribution margin per unit of constrained resource by dividing each product’s contribution margin per unit by the amount of constrained resource needed to make it. For example, divide the contribution margin of each product by the number of units of grill time needed.
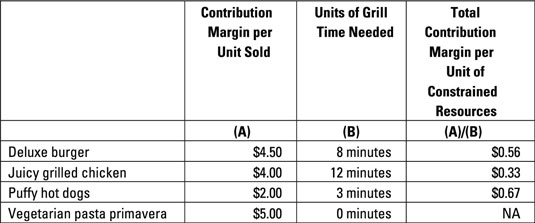
If Charlie’s cook is making Juicy Grilled Chicken, each unit of grill time yields only $0.33 worth of contribution margin. When he’s cooking Puffy Hot Dogs, each unit of grill time yields $0.67. Cooking Deluxe Burgers results in $0.56 of contribution margin per unit of grill time.
Therefore, if grill time is constrained, Charlie’s wants to sell as many Puffy Hot Dogs as possible because they have the highest contribution margin per unit of constrained resource (a staggering $0.67 per unit of grill time).
The cook should then dedicate any remaining grill space to Deluxe Burgers ($0.56 per unit of grill time). If the restaurant can meet the demand for hot dogs and deluxe burgers, the cook can make room for the Juicy Grilled Chicken. (If not, he may just want to pretend he’s run out of chicken.)
Now don’t forget the Vegetarian Pasta Primavera. Because this dish doesn’t require any time on the grill at all, it offers the most effective way around the constraint. Even though the grill limits your production and sales of hamburgers, chicken, and hot dogs, it can’t limit your production and sales of Vegetarian Pasta Primavera. It’s the perfect candidate for Special of the Day.
A useful management tool called the theory of constraints provides more advanced techniques to help managers maximize the benefits from limited resources.





