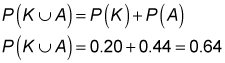You use the addition rule to compute the probability of the union of two events. Mathematically speaking, for events A and B, the addition rule states that
This shows that the probability of the union of events A and B equals the sum of the probability of A and the probability of B, from which the probability of both events is subtracted. Subtracting the probability of both events is necessary to avoid the problem of double-counting. This is shown in the following example:
Suppose that event A contains the elements 1, 2, 3 and event B contains the elements 3, 4, 5. The sample space contains the elements 1, 2, 3, 4, 5.
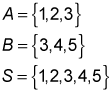
The corresponding probabilities are:
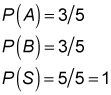
The union of A and B contains all the elements in the sample space:
As a result, the probability of A union B equals 1. (Recall that the sample space always has a probability of 1.) If you simply combine the probabilities of A and B, though, you will get a surprising result; they sum to 6/5, which is greater than 1.
This result occurs because the element 3 appears in both A and B:
The probability of 3 was counted twice, once in set A and once in set B, which accounts for the sum of the probabilities being greater than one. By subtracting the probability of the element 3, the correct probability of 1 is found.
The table shows the distribution of coffees (measured in pounds) the Big Bean Corporation produces during a given day.
| Coffee Styles | Special Reserve Blend (S) | Kona Hawaii Blend (K) | Aromatic Blend (A) | Total |
|---|---|---|---|---|
| Decaffeinated (D) | 0.12 | 0.80 | 0.22 | 0.42 |
| Regular (R) | 0.24 | 0.12 | 0.22 | 0.58 |
| Total | 0.36 | 0.20 | 0.44 | 1.00 |
If you choose a pound of coffee randomly from the daily output of the Big Bean Corporation, what's the probability that it's either the Special Reserve Blend (S) or the Regular (R) (or both)?
In this example, you use the addition rule because you're being asked to compute the probability of a union. You combine the probability of S with the probability of R, subtracting the intersection between them to avoid the problem of double-counting.
From the table, you can determine that P(S) = 0.36; that P(R) = 0.58;

Seventy percent of the coffee produced by Big Bean is the special reserve blend, regular, or both.
When two events A and B are mutually exclusive (that is, they can't both occur at the same time), the addition rule simplifies to
For example, if you choose a pound of coffee randomly from the daily output of the Big Bean Corporation, what's the probability that it's either the Kona Hawaii Blend (K) or the Aromatic Blend (A)?
Because a pound of coffee can't be both the Kona Hawaii Blend and the Aromatic Blend, events K and A are mutually exclusive. This means that you can use the simplified version of the addition rule: