As with all of the other subtests on the ASVAB, guessing on the Mathematics Knowledge subtest doesn’t count against you. (unless you guess your way through the questions at the end of the test and get several of them wrong. Then you may be penalized for mismanaging your time.)
So scribble in an answer, any answer, on your answer sheet because, if you don’t, your chances of getting that answer right are zero. But if you take a shot at it, your chances increase to 25%, or 1 in 4.
Knowing what the question is asking
The Mathematics Knowledge subtest presents the questions as straightforward math problems, not word problems, so knowing what the question is asking you to do is relatively easy. However, reading each question carefully, paying particular attention to plus (+) and minus (–) signs (which can really change the answer), is still important. Finally, make sure you do all the calculations needed to produce the correct answer. Check out this example:
Find the value of
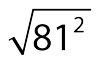
(A) 9
(B) 18
(C) 81
(D) 6,561
If you’re in a hurry, you may put 9 down as an answer because you remember that the square root of 81 is 9. Or in a rush, you could multiply 9 (the square root of 81) by 2 instead of squaring it, as the exponent indicates you should. Or you may just multiply 81 by 81 to get 6,561 without remembering that you also need to then find the square root, which gives you the correct answer, Choice (C).
So make sure you perform all the operations needed (and that you perform the correct operations) to find the right answer. Here, noticing that you’re both squaring 81 and taking the square root of 812 should make it easy for you to recognize that the answer is actually just 81, without having to work out the multiplication.
Figuring out what you’re solving for
Right out of the gate, read the question carefully. Some questions can seem out of your league at first glance, but if you look at them again, a light may go on in your brain. Suppose you get this question:
Solve for s:
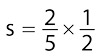
(A) 2 1/2
(B) 2
(C) 1/5
(D) 1/10
At first glance, you may think, “Oh, no! Solve for an unknown, s. I don’t remember how to do that!” But if you look at the question again, you may see that you’re not solving for s at all. You’re simply multiplying a fraction. So you take 2/5 times 1/2 and arrive at 2/10, but you should reduce that fraction to get 1/5. The correct answer is Choice (C).
Solving what you can and guessing the rest
Sometimes a problem requires multiple operations for you to arrive at the correct answer. If you don’t know how to do all of the operations, don’t give up. You can still narrow down your choices by doing what you can.
Suppose this question confronts you:
What’s the value of (0.03)3
(A) 0.0027
(B) 0.06
(C) 0.000027
(D) 0.0009
Say you don’t remember how to multiply decimals. All isn’t lost! If you remember how to use exponents, you know that you have to multiply 0.03 × 0.03 × 0.03. So if you simplify the problem and just multiply 3 × 3 × 3, without worrying about those pesky zeros, your answer will have a 27 in it. With this pearl of wisdom in mind, you can see that Choice (B), which adds 0.03 to 0.03, is wrong.
It also means that Choice (D), which multiplies 0.03 and 0.03, is wrong. Now you have two possible answers, and you’ve improved your chances of guessing the right one to 50 percent! Multiply 3 × 3 × 3 to get 27, and don’t forget to put the decimal points back in. You have six places to make up, so move the decimal from 27 six places to the left to get 0.000027. The correct answer is Choice (C).
Using the process of elimination
Another method for when you run into questions and draw a total blank is to plug the possible answers into the equation and see which one works. Say the following problem is staring you right in the eyes:
Solve for x: x – 5 = 32
(A) x= 5
(B) x = 32
(C) x= -32
(D) x = 37
If you’re totally stumped and can’t think of any possible way of approaching this problem, simply plugging in each of the four answers to see which one is correct is your best bet. Answer D is correct.
Don’t forget that plugging in all the answers is time-consuming, so save this procedure until you’ve answered all the problems you can answer. If you’re taking the computer version, you can’t skip a question, so remember to budget your time wisely. If you don’t have much time, just make a guess and move on. You may be able to solve the next question easily.





