This article takes a look at a 3D potential that forms a box, as you see in the following figure. You want to get the wave functions and the energy levels here.
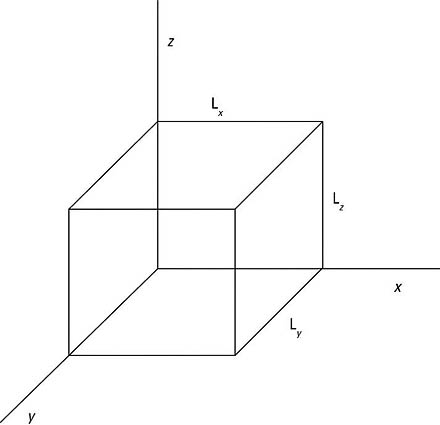
Inside the box, say that V(x, y, z) = 0, and outside the box, say that
So you have the following:
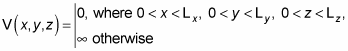
Dividing V(x, y, z) into Vx(x), Vy(y), and Vz(z) gives you
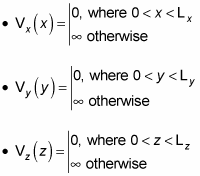
Okay, because the potential goes to infinity at the walls of the box, the wave function,
must go to zero at the walls, so that's your constraint. In 3D, the Schrödinger equation looks like this in three dimensions:
Writing this out gives you the following:
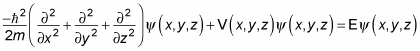
Take this dimension by dimension. Because the potential is separable, you can write
Inside the box, the potential equals zero, so the Schrödinger equation looks like this for x, y, and z:
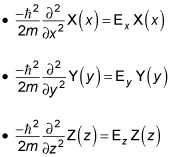
The next step is to rewrite these equations in terms of the wave number, k. Because
you can write the Schrödinger equations for x, y, and z as the following equations:
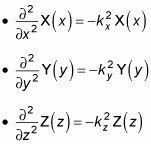
Start by taking a look at the equation for x. Now you have something to work with — a second order differential equation,
Here are the two independent solutions to this equation, where A and B are yet to be determined:
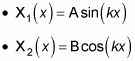
So the general solution of
is the sum of the last two equations:





