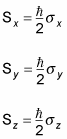In quantum physics, when you work with spin eigenstates and operators for particles of spin 1/2 in terms of matrices, you may see the operators Sx, Sy, and Sz written in terms of Pauli matrices,
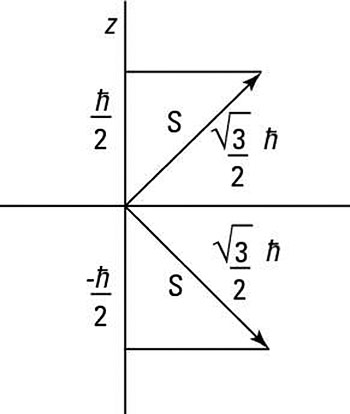
Given that the eigenvalues of the S2 operator are
and the eigenvalues of the Sz operator are
you can represent these two equations graphically as shown in the following figure, where the two spin states have different projections along the z axis.
Here’s what the Pauli matrices look like for the operators Sx, Sy, and Sz:
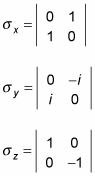
Now you can write Sx, Sy, and Sz in terms of the Pauli matrices like this: