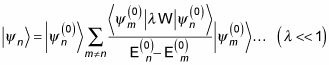How to Find the First-Order Corrections to Energy Levels and Wave Functions

In quantum physics, in order to find the first-order corrections to energy levels and wave functions of a perturbed system, E_n, you need to calculate E⁽¹⁾_n, as well as

So how do you do that? You start with three perturbed equations:

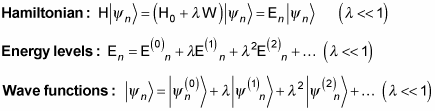
You then combine these three equations to get this jumbo equation:

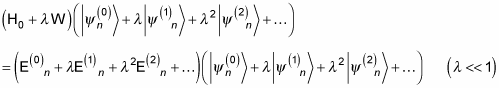
You can handle the jumbo equation by setting the coefficients of lambda on either side of the equal sign to each other. After matching the coefficients of lambda and simplifying, you can find the first-order correction to the energy, E⁽¹⁾_n, by multiplying

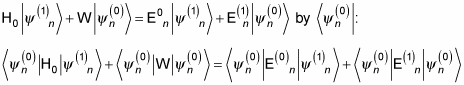
Then the first term can be neglected and you can use simplification to write the first-order energy perturbation as:

Swell, that's the expression you use for the first-order correction, E⁽¹⁾_n.

Now look into finding the first-order correction to the wave function,

You can multiply the wave-function equation by this next expression, which is equal to 1:

So you have

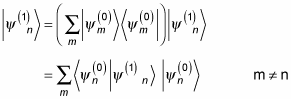
Note that the m = n term is zero because

So what is

You can find out by multiplying the first-order correction,

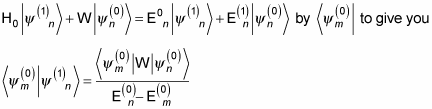
And substituting that into

gives you

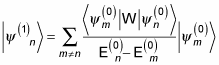
Okay, that's your term for the first-order correction to the wave function,

The wave function looks like this, made up of zeroth-, first-, and second-order corrections:

Ignoring the second-order correction and substituting

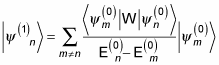
in for the first-order correction gives you this for the wave function of the perturbed system, to the first order: