Given that everything in quantum physics is done in terms of probabilities, making predictions becomes very important. And the biggest such prediction is the expectation value. The expectation value of an operator is the average value that you would measure if you performed the measurement many times. For example, the expectation value of the Hamiltonian operator is the average energy of the system you’re studying.
The expectation value is a weighted average of the probabilities of the system being in its various possible states. Here’s how you find the expectation value of an operator A:
Note that because you can express
as a row vector and
as a column vector, you can express the operator A as a square matrix.
For example, suppose you’re working with a pair of dice and the probabilities of all the possible sums. In this situation, the expectation value is a sum of terms, and each term is a value that can be displayed by the dice, multiplied by the probability that that value will appear.
The bra and ket will handle the probabilities, so it’s up to the operator that you create for this — call it the Roll operator, R — to store the dice values (2 through 12) for each probability. Therefore, the operator R looks like this:

So to find the expectation value of R, you need to calculate
Spelling that out in terms of components gives you the following:
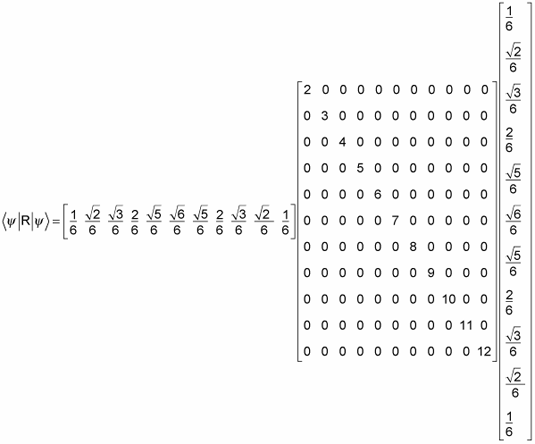
Doing the math, you get
So the expectation value of a roll of the dice is 7. Now you can see where the terms bra and ket come from — they “bracket” an operator to give you expectation values. In fact, the expectation value is such a common thing to find that you’ll often find
abbreviated as





