How to Decouple Different Particles into Linearly Independent Equations

In quantum physics, you can decouple systems of particles that you can distinguish — that is, systems of identifiably different particles — into linearly independent equations. To illustrate this, suppose you have a system of many different types of cars floating around in space. You can distinguish all those cars because they’re all different — they have different masses, for one thing.

Now say that each car interacts with its own potential — that is, the potential that any one car sees doesn’t depend on any other car. That means that the potential for all cars is just the sum of the individual potentials each car sees, which looks like this, assuming you have N cars:

Being able to cut the potential energy up into a sum of independent terms like this makes life a lot easier. Here’s what the Hamiltonian looks like:

Notice how much simpler this equation is than this Hamiltonian for the hydrogen atom:

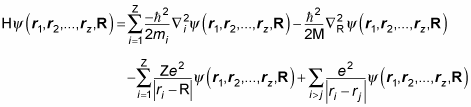
Note that you can separate the previous equation for the potential of all cars into N different equations:

And the total energy is just the sum of the energies of the individual cars:

And the wave function is just the product of the individual wave functions:

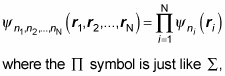
except it stands for a product of terms, not a sum, and n_i refers to all the quantum numbers of the ith particle.

As you can see, when the particles you’re working with are distinguishable and subject to independent potentials, the problem of handling many of them becomes simpler. You can break the system up into N independent one-particle systems. The total energy is just the sum of the individual energies of each particle. The Schrödinger equation breaks down into N different equations. And the wave function ends up just being the product of the wave functions of the N different particles.

Take a look at an example. Say you have four particles, each with a different mass, in a square well. You want to find the energy and the wave function of this system. Here’s what the potential of the square well looks like this for each of the four noninteracting particles:

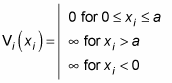
Here’s what the Schrödinger equation looks like:

You can separate the preceding equation into four one-particle equations:

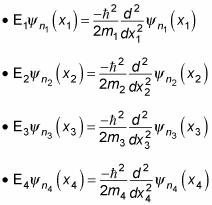
The energy levels are

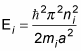
And because the total energy is the sum of the individual energies is

the energy in general is

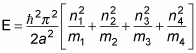
So here’s the energy of the ground state — where all particles are in their ground states, n₁ = n₂ = n₃ = n₄ = 1:

For a one-dimensional system with a particle in a square well, the wave function is

The wave function for the four-particle system is just the product of the individual wave functions, so it looks like this:

For example, for the ground state, n₁ = n₂ = n₃ = n₄ = 1, you have

So as you can see, systems of N independent, distinguishable particles are often susceptible to solution — all you have to do is to break them up into N independent equations.