In quantum physics, to find the actual eigenfunctions (not just the eigenstates) of angular momentum operators like L2 and Lz, you turn from rectangular coordinates, x, y, and z, to spherical coordinates because it’ll make the math much simpler (after all, angular momentum is about things going around in circles). The following figure shows the spherical coordinate system.
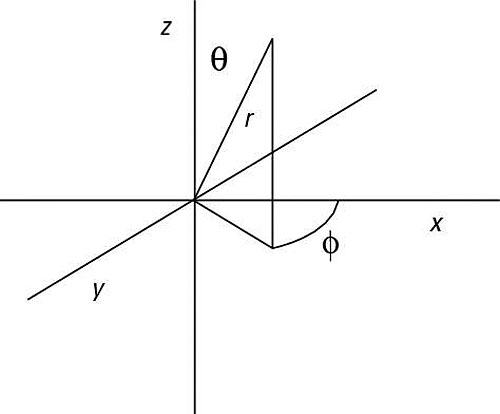
In the rectangular (Cartesian) coordinate system, you use x, y, and z to orient yourself. In the spherical coordinate system, you also use three quantities:
as the figure shows. You can translate between the spherical coordinate system and the rectangular one this way: The r vector is length of the vector to the particle that has angular momentum,
is the angle of r from the z axis, and
is the angle of r from the x axis.

Consider the equations for angular momentum:
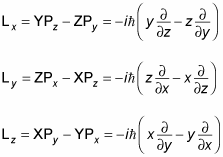
When you take the angular momentum equations with the spherical-coordinate-system conversion equations, you can derive the following:
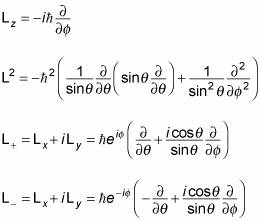
Okay, these equations look pretty involved. But there’s one thing to notice: They depend only on
which means their eigenstates depend only on
not on r. So the eigenfunctions of the operators in the preceding list can be denoted like this:
Traditionally, you give the name
to the eigenfunctions of angular momentum in spherical coordinates, so you have the following:
All right, time to work on finding the actual form of
You know that when you use the L2 and Lz operators on angular momentum eigenstates, you get this:
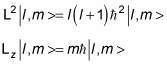
So the following must be true:
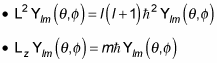
In fact, you can go further. Note that Lz depends only on
which suggests that you can split
up into a part that depends on
and a part that depends on
Splitting
up into parts looks like this:
That’s what makes working with spherical coordinates so helpful — you can split the eigenfunctions up into two parts, one that depends only on
and one part that depends only on





