Applying the Spherical Bessel and Neumann Functions to a Free Particle

In quantum physics, you can apply the spherical Bessel and Neumann functions to a free particle (a particle which is not constrained by any potential). The wave function in spherical coordinates takes this form:

and

gives you the spherical harmonics. The problem is now to solve for the radial part, R_nl(r). Here's the radial equation:

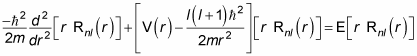
For a free particle, V(r) = 0, so the radial equation becomes

The way you usually handle this equation is to substitute

and because you have a version of the same equation for each n index it is convenient to simply remove it, so that R_nl (r) becomes

This substitution means that

becomes the following:

The radial part of the equation looks tough, but the solutions turn out to be well-known — this equation is called the spherical Bessel equation, and the solution is a combination of the spherical Bessel functions

and the spherical Neumann functions

where A_l and B_l are constants. So what are the spherical Bessel functions and the spherical Neumann functions? The spherical Bessel functions are given by

Here's what the first few iterations of

look like:

How about the spherical Neumann functions? The spherical Neumann functions are given by

Here are the first few iterations of