In physics, you can use the vertical-loop velocity equation to determine the speed needed to go around a vertical loop. You can also use it to determine the diameter of, for example, a rollercoaster loop.
Here are some practice questions that you can try.
Practice questions
A 20-gram mouse is running in a stationary, vertical wheel of diameter 15 centimeters. How fast must the mouse run to make it all the way around the loop without falling upside down to the bottom of the wheel?
Round your answer to the nearest hundredth of a meter per second.
The Circle o' Death roller coaster has a loop-the-loop with a minimum speed requirement at the top of 126 kilometers per hour to prevent the cart from losing contact with the coaster's track. What is the diameter of the loop?
Round your answer to the nearest hundredth of a kilometer.
Answers
The following are the answers to the practice questions:
0.86 m/s
Before you use the vertical-loop velocity equation
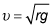
(where r is the radius of the loop and g is the gravitational acceleration on Earth's surface), you need to find the radius from the diameter in the correct units. Radius is half the diameter, or 7.5 centimeters. Converting to meters yields
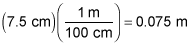
Therefore, the minimum velocity the mouse needs to make it past the top of the loop without falling is:

0.25 km
To use the vertical-loop velocity formula,
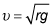
you need to first convert the given velocity to units of meters per second (to match the meters per second squared of g):
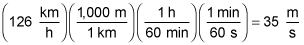
Therefore:
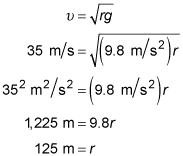
Finally, multiply by 2 to get the diameter and then convert to kilometers and round to the nearest hundredth:


