In physics, tracking simple harmonic motion can require time and patience when you have to figure out how the motion of an object changes over time.
Imagine that one day you come up with a brilliant idea for an experimental apparatus. You decide to shine a spotlight on a ball bouncing on a spring, casting a shadow on a moving piece of photographic film. Because the film is moving, you get a record of the ball’s motion as time goes on. You turn the apparatus on and let it do its thing; the results are shown in the first figure.
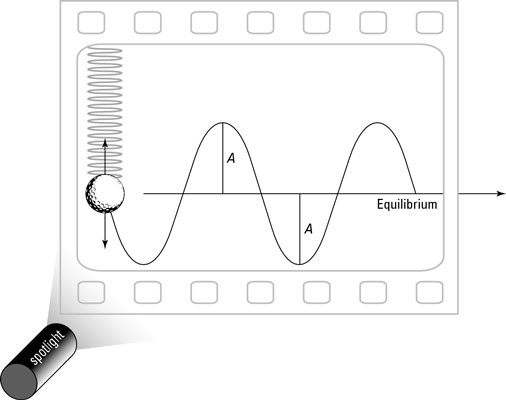
The ball oscillates around the equilibrium position, up and down, reaching amplitude A at its lowest and highest points. But take a look at the ball’s track: You can tell where the ball is moving fastest because that’s where the curve has the steepest slope. The ball goes fastest near the equilibrium point because of the acceleration caused by the spring force, which has been applied since the turning point. At the top and bottom, the ball is subject to plenty of force from the spring, so it slows down and reverses its motion.
The track of the ball is best modeled with a sine wave, which means that its track is a sine wave of amplitude A. (Note: You can also use a cosine wave, because the shape is the same. The only difference is that when a sine wave is at its peak, the cosine wave is at zero, and vice versa.)
You can get a clear picture of the sine wave if you plot the sine function on an xy graph like this:
y = sin x
Now take a look at the sine wave in a circular way.
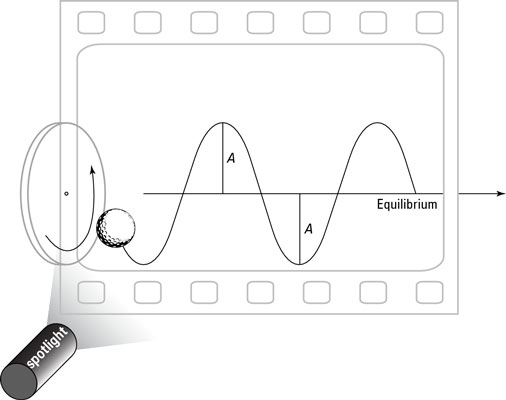
If you attach a ball to a rotating disk, as the second figure shows, and you shine a spotlight on it, you get the same result as when you have the ball hanging from the spring (see the first figure): a sine wave.
The rotating disk, which you can see in the third figure, is often called a reference circle. You can see how the vertical component of circular motion relates to the sinusoidal (sine-like) wave of simple harmonic motion. Reference circles can tell you a lot about simple harmonic motion.
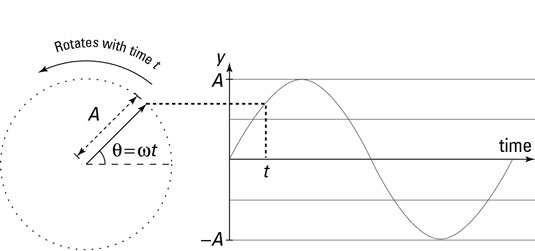
As the disk turns, the angle, theta, increases in time. What does the track of the ball look like as the film moves to the right? Using a little trig, you can resolve the ball’s motion along the y-axis; all you need is the vertical (y) component of the ball’s position. At any one time, the ball’s y position is the following:
The vertical displacement varies from positive A to negative A in amplitude.
velocity along the axis of rotation of the disk — and t is time:
You can now explain the track of the ball as time goes on, given that the disk is rotating with angular velocity





