In physics, if you know the kinetic and potential energies that act on an object, then you can calculate the mechanical energy of the object. Imagine a roller coaster car traveling along a straight stretch of track. The car has mechanical energy because of its motion: kinetic energy. Imagine that the track has a hill and that the car has just enough energy to get to the top before it descends the other side, back down to a straight and level track (see the figure). What happens?
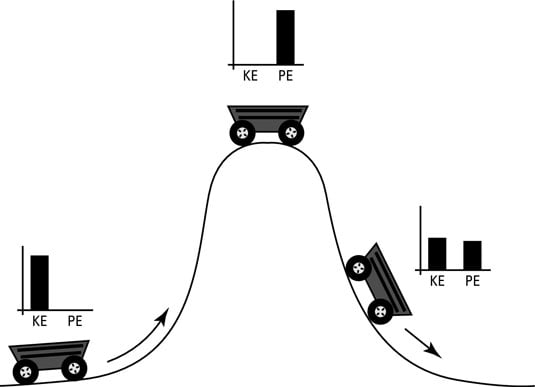
Well, at the top of the hill, the car is pretty much stationary, so where has all its kinetic energy gone? The answer is that it has been converted to potential energy. As the car begins its descent on the other side of the hill, the potential energy begins to be converted back to kinetic energy, and the car gathers speed until it reaches the bottom of the hill. Back at the bottom, all the potential energy the car had at the top of the hill has been converted back into kinetic energy.
An object’s mechanical potential energy derives from work done by forces, and a label for a particular potential energy comes from the forces that are its source. For example, the roller coaster has potential energy because of the gravitational forces acting on it, so this is often called gravitational potential energy.
The roller coaster car’s total mechanical energy, which is the sum of its kinetic and potential energies, remains constant at all points of the track (ignoring frictional forces). The combination of the kinetic and potential energies does vary, however. When the only work done on an object is performed by conservative forces, its mechanical energy remains constant, whatever motions it may undergo.
Say, for example, that you see a roller coaster at two different points on a track — Point 1 and Point 2 — so that the coaster is at two different heights and two different speeds at those points. Because mechanical energy is the sum of the potential energy
and kinetic energy
the total mechanical energy at Point 1 is
At Point 2, the total mechanical energy is
What’s the difference between ME2 and ME1? If there’s no friction (or another nonconservative force), then ME1 = ME2, or
These equations represent the principle of conservation of mechanical energy. The principle says that if the net work done by nonconservative forces is zero, the total mechanical energy of an object is conserved; that is, it doesn’t change. (If, on the other hand, friction or another nonconservative force is present, the difference between ME2 and ME1 is equal to the net work the nonconservative forces do: ME2 – ME1 = Wnc.)
Another way of rattling off the principle of conservation of mechanical energy is that at Point 1 and Point 2,
PE1 + KE1 = PE2 + KE2
You can simplify that mouthful to the following:
ME1 = ME2
where ME is the total mechanical energy at any one point. In other words, an object always has the same amount of energy as long as the net work done by nonconservative forces is zero.
You can cancel out the mass, m, in the previous equation, which means that if you know three of the values (heights and velocities), you can solve for the fourth:

