In some types of collisions, called elastic collisions, kinetic energy and momentum are conserved. What do elastic collisions look like? In general, there’s no permanent deformation of any of the objects from an elastic collision. The objects involved might initially deform, but they immediately spring back to their original shape. Here are the equations for the conservation of these factors:
KEo = KEf
po = pf
Check out this idea in action: Suppose that you’re in a car when you hit the car in front of you (elastically — no deformation of bumpers is involved), which started at rest. You know that momentum is always conserved, and you know that the car in front of you was stopped when you hit it, so if your car is car 1 and the other one is car 2, you get this equation:
m1vf1 +m2vf2 = m1vo1
This equation can’t tell you what vf1 and vf2 are, because there are two unknowns and only one equation. You can’t solve for either vf1 or vf2 exactly in this case, even if you know the masses and vo1. So to solve for both final speeds, you need another equation to constrain what’s going on here. That means using the conservation of kinetic energy.
The collision was an elastic one, so kinetic energy was indeed conserved. That means that
With two equations and two unknowns, vf1 and vf2, you can solve for those unknowns in terms of the masses and vo1.
You probably won’t be asked to solve questions of this kind on physics tests because, in addition to being two simultaneous equations, the second equation has a lot of squared velocities in it. But it’s one you may see in homework. When you do the math, you get
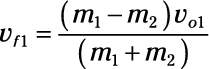
and
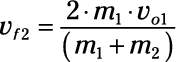
This is a more substantial result than you get from problems that just use the conservation of momentum; in such problems, you can solve for only one final speed. Here, using both the conservation of momentum and kinetic energy, you can solve for both objects’ final speeds.
However, remember that the formulas in this section work only in the special case of an elastic collision. Also, the formulas would need to be modified if the initial velocity of the second object wasn’t zero.
Sample question
You’re in a car that hits the at-rest car in front of you. If you and your car’s mass is 1,000.0 kg, the mass of the car and driver ahead of you is 900.0 kg, and if you started at 44 m/s, what are the final speeds of the two cars?
Assume that the collision is elastic and all the action happens in the same line as your original direction of travel.
The correct answer is that your car moves 2.3 m/s, and the other car moves 46 m/s.
You know that this collision is elastic and the second car starts at rest, so you can use the equations given earlier in this section. Use this equation to find the final speed of your car:
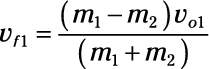
Plug in the numbers:

Use this equation to find the final speed of the other car:

Plug in the numbers:

Practice questions
A 160-g hockey puck traveling at 60.0 m/s hits a stationary puck with the same mass. What are the final speeds of the pucks, given that the collision is elastic and that all motion takes place along the same line?
You’re driving a bumper car at 23 m/s, and you hit another bumper car that’s at rest. If you and your car have a mass of 300 kg, and the mass of the other car and driver is 240 kg, what are the final speeds of the cars?
Following are answers to the practice questions:
0, 60 m/s
Use this equation to find the final speed of the first puck:
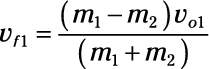
Substituting the numbers gives you:

Use this equation to find the final speed of the second puck:

Putting in the numbers gives you:

Note that when the masses are the same, the first puck stops, and the second puck takes off with the same speed as the first puck had.
You: 2.6 m/s; the other car: 26 m/s
Use this equation to find the final speed of your car:
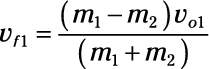
Plug in the numbers:

Use this equation to find the final speed of the second car:

Plug in the numbers:






