When you have two sides of a triangle and the angle between them, otherwise known as SAS (side-angle-side), you can use the law of cosines to solve for the other three parts. Consider the triangle ABC where a is 15, c is 20, and angle B is 124 degrees. The following figure shows what this triangle looks like.
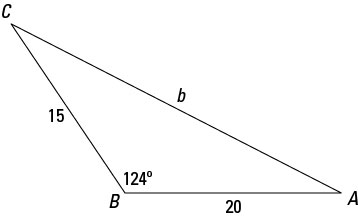
Now, to solve for the measure of the missing side and angles:
Find the measure of the missing side by using the law of cosines.
Use the law that solves for side b.

You end up with the value for b2. Take the square root of each side and just use the positive value (because a negative length doesn’t exist).

The length of side b is about 31.
Find the measure of one of the missing angles by using the law of cosines.
Using the law that solves for a, fill in the values that you know.

Solve for cos A by simplifying and moving all the other terms to the left.

Using a scientific calculator to find angle A, you find that A = cos–1(0.916) = 23.652, or about 24 degrees.
You can also switch to the law of sines to solve for this angle. Don’t be afraid to mix and match when solving these triangles.
Find the measure of the last angle.
Determine angle B by adding the other two angle measures together and subtracting that sum from 180.
180 – (124 + 24) = 180 – 148 = 32. Angle B measures 32 degrees.
How about an application that uses this SAS portion of the law of cosines? Consider the situation: A friend wants to build a stadium in the shape of a regular pentagon (five sides, all the same length) that measures 920 feet on each side. How far is the center of the stadium from the corners? The left part of figure shows a picture of the stadium and the segment you’re solving for.
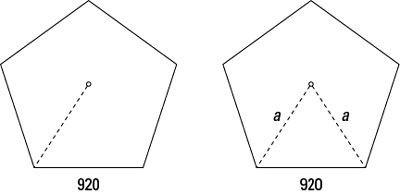
You can divide the pentagon into five isosceles triangles. The base of each triangle is 920 feet, and the two sides are equal, so call them both a. Refer to the right-hand picture in the preceding figure. Use the law of cosines to solve for a, because you can get the angle between those two congruent sides, plus you already know the length of the side opposite that angle.
Determine the measure of the angle at the center of the pentagon.
A circle has a total of 360 degrees. Divide that number by 5, and you find that the angle of each triangle at the center of the pentagon is 72 degrees.
Use the law of cosines with the side measuring 920 feet being the side solved for.

Because the other two sides are the same measure, write them both as a in the equation.
Solve for the value of a.

The distance from the center to a corner is between 782 and 783 feet.
The computations here involve using rounded values. It’s usually best to hold off doing the rounding until you’re ready to report your final answer. In these cases, it didn’t really matter, but you want to be cautious if more accuracy is needed.





