You can use trigonometry to graph the changes in high and low tides for a particular location. Along the coast, the tides are of particular interest. They are affected by the gravitational pull of both the moon and the sun. The high tides and low tides follow a periodic pattern that you can model with the sine function.
For example, on a particular winter day, the high tide in Boston, Massachusetts, occurred at midnight. To determine the height of the water in the harbor, use the equation
where t represents the number of hours since midnight.
Input the value of t into the equation to find the height at a particular time.
At midnight, the value of t is 0. Putting 0 in for t in the equation gives you

The greatest value of sine occurs at
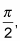
so it makes sense that high tide would be when the formula uses the sine of that value.
Determine the change in the height using the amplitude.
The multiplier of 4.8 is the amplitude — how far above and below the middle value that the graph goes. The tides go 4.8 feet above and below the average amount on this particular day. The number added on at the end, 5.1, is the average height for the tides. So the tide goes up to 9.9 feet and down to 0.3 feet — wading depth.
Find the time between high tides with the period of the function.

The period is 12 hours, so you know that the tides go through their entire cycle in 12 hours. The 3 added to the t is a shift horizontally; that number determines what times of day the high tide and low tide occur.
 The tides in Boston on one wintry day.
The tides in Boston on one wintry day.The figure shows a graph of this function and the different stages of the tide at different times. By looking at the graph, you can plan your sailing and clam-digging activities.





