You can find function values of angles using angle-addition identities. And you have more possibilities for finding the function values of angles when you use subtraction in a trig problem. For example, you can determine the sine of 15 degrees by using 45 degrees and 30 degrees and the appropriate function values and identity.
The subtraction, or difference, identities find the function for the difference between angles α and β:
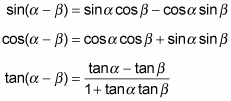
Notice how each of the subtraction identities resembles its corresponding angle-sum identity. For the sine rule, the sign between the two products changed from + to –, which seems to make sense. The opposite is true for cosine. The addition rule for cosine has – in it, and the subtraction (or difference) rule has + in it. The tangent rule has both + and – in it; the operation in the numerator mirrors the type of identity.
Only the original three trig functions have truly usable difference identities — the identities for the reciprocal functions are pretty darned complicated. If you want the difference of a reciprocal function, your best bet is to use the corresponding basic identity and find the reciprocal of the numerical answer after you're all finished.
To see one of the subtraction identities in action, check out the following example, which shows how you can find the sine of 15 degrees.
Determine two angles with a difference of 15 degrees.
To keep things simple, use 45 and 30.
Substitute the angles into the identity for the sine of a difference.

Replace the terms with the function values and simplify the answer.

Using radians introduces fractions to the picture, such as finding tan π/12 by using the identity for the tangent of a difference.
Determine which angles you need to get the difference.

Substitute the angles into the identity for the tangent of a difference.

Replace the terms with the function values and simplify the answer.

The result is rather messy. You can simplify it even more by multiplying the numerator and denominator by the conjugate (same terms, different sign) of the denominator and simplifying the result:

This next example uses the identity for the cosine of a difference along with the angle measuring 0 degrees to determine an opposite-angle identity. It shows how versatile and user-friendly trig identities are — and how they all get along so well together.
In this example, find
by using the identity for the difference between angles.
Determine which angles you need to get the difference.
Using 0 and π/3 and subtracting with the 0 first gives a negative result:

Substitute the angles into the identity for the cosine of a difference.

Replace the angles with the function values and simplify the answer.

This answer is exactly what you get if you use the opposite-angle identity for cosine:






