Using radians is very helpful when you are doing trigonometry applications involving the length of an arc of a circle, which is part of its circumference. This might include measuring the sweep of a hand on a clock or finding the distance in a navigation problem.
A part of a circle may be an arc, a diameter (not really a physical part, but a measure), a sector (a pie-piece of the inside), or the center. The measures usually start out in degrees, and you change them to radians, when necessary, to complete the problem.
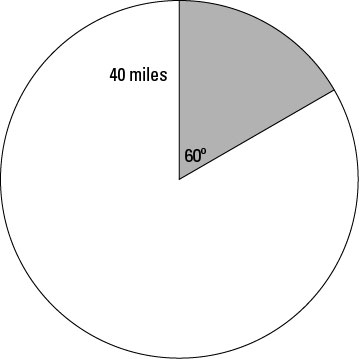
For example, radar scans a circular area that has a radius of 40 miles. In one second, it sweeps an arc of 60 degrees. What area does the radar cover in one second? In five seconds? Refer to the preceding figure, which shows a sweep of 60 degrees.
Here’s how you solve this problem:
-
Find the area of the circle.

-
Divide by the portion of the circle that the sweep covers.
The sweep of 60 degrees is only one-sixth of the entire circle, so you figure the area that the sweep covers by dividing the entire area by 6.

The preceding problem works out nicely, because the number of degrees (60) is a convenient value — it’s a fraction of the circle. But what if the number doesn’t divide evenly into 360? For example, what if the radar sweeps an angle of 76 degrees in one second?

Take the fraction for that part of the circle and multiply it by the area, πr2. A fancy name for this part of a circle is sector.
Keep the following formulas in mind when you’re trying to find the area of a sector:

For example, to find the area of the radar sweep in the preceding example when the radar sweeps 76 degrees per second, follow these steps:
-
Put 76 in for the θ° and 40 for the radius in the formula for the area of a sector.

-
Multiply and divide to simplify the answer.

To demonstrate this radar-sweep calculation if you're given measurements in radians, find the area of the radar sweep if the sweep is π/3 radians (which is 60 degrees).
-
Put π/3 in for the θR and 40 in for the radius.

-
Multiply and divide to simplify the answer.






