Although the normal (Z-) distribution and t-distribution are similar, they look different from each other and are used for different statistical purposes. The normal distribution is that well-known bell-shaped distribution whose mean is
and whose standard deviation is
The standard normal (or Z-distribution), is the most common normal distribution, with a mean of 0 and standard deviation of 1. The t-distribution can be thought of as a cousin of the standard normal distribution — it looks similar in that it's centered at zero and has a basic bell-shape, but it's shorter and flatter around the center than the Z-distribution. Its standard deviation is proportionally larger compared to the Z, which is why you see the fatter tails on each side.
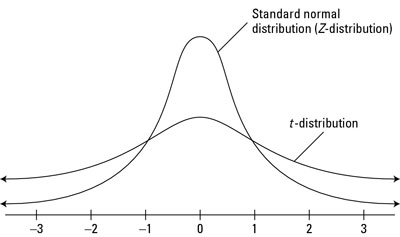
This figure compares the t- and standard normal (Z-) distributions in their most general forms.
The t-distribution is typically used to study the mean of a population, rather than to study the individuals within a population. In particular, it is used in many cases when you use data to estimate the population mean — for example, using the sample mean of 20 homes to estimate the average price of all the new homes in California. Or when you use data to test someone's claim about the population mean — for example, is it true that the mean price of all the new homes in California is $500,000?
The connection between the normal distribution and the t-distribution is that the t-distribution is often used for analyzing the mean of a population if the population has a normal distribution (or fairly close to it). Its role is especially important if your data set is small or if you don't know the standard deviation of the population (which is often the case).
When statisticians use the term t-distribution, they aren't talking about just one individual distribution. There is an entire family of specific t-distributions, depending on what sample size is being used to study the population mean. Each t-distribution is distinguished by what statisticians call its degrees of freedom. In situations where you have one population and your sample size is n, the degrees of freedom for the corresponding t-distribution is n – 1. For example, a sample of size 10 uses a t-distribution with 10 – 1, or 9, degrees of freedom, denoted t9 (pronounced tee sub-nine). Situations involving two populations use different degrees of freedom.





