To estimate the difference between two population proportions with a confidence interval, you can use the Central Limit Theorem when the sample sizes are large enough (typically, each at least 30). When a statistical characteristic, such as opinion on an issue (support/don’t support), of the two groups being compared is categorical, people want to report on the differences between the two population proportions — for example, the difference between the proportion of women and men who support a four-day work week. How do you do this?
You estimate the difference between two population proportions, p1 – p2, by taking a sample from each population and using the difference of the two sample proportions,
plus or minus a margin of error. The result is called a confidence interval for the difference of two population proportions, p1 – p2.
The formula for a confidence interval (CI) for the difference between two population proportions is
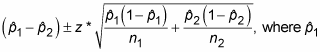
and n1are the sample proportion and sample size of the first sample, and
and n2are the sample proportion and sample size of the second sample. The value z* is the appropriate value from the standard normal distribution for your desired confidence level. (Refer to the following table for z*-values.)
| z*-values for Various Confidence Levels | |
| Confidence Level | z*-value |
|---|---|
| 80% | 1.28 |
| 90% | 1.645 (by convention) |
| 95% | 1.96 |
| 98% | 2.33 |
| 99% | 2.58 |
To calculate a CI for the difference between two population proportions, do the following:
Determine the confidence level and find the appropriate z*-value.
Refer to the above table.
Find the sample proportion

for the first sample by taking the total number from the first sample that are in the category of interest and dividing by the sample size, n1. Similarly, find
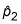
for the second sample.
Take the difference between the sample proportions,
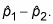
Find

and divide that by n1. Find

and divide that by n2. Add these two results together and take the square root.
Multiply z* times the result from Step 4.
This step gives you the margin of error.
Take

plus or minus the margin of error from Step 5 to obtain the CI.
The lower end of the CI is

minus the margin of error, and the upper end of the CI is

plus the margin of error.
The formula shown here for a CI for p1 – p2 is used under the condition that both of the sample sizes are large enough for the Central Limit Theorem to be applied and allow you to use a z*-value; this is true when you are estimating proportions using large scale surveys, for example. For small sample sizes, confidence intervals are beyond the scope of an intro statistics course.
Suppose you work for the Las Vegas Chamber of Commerce, and you want to estimate with 95% confidence the difference between the percentage of all females who have ever gone to see an Elvis impersonator and the percentage of all males who have ever gone to see an Elvis impersonator, in order to help determine how you should market your entertainment offerings.
Because you want a 95% confidence interval, your z*-value is 1.96.
Suppose your random sample of 100 females includes 53 females who have seen an Elvis impersonator, so

is 53 divided by 100 = 0.53. Suppose also that your random sample of 110 males includes 37 males who have ever seen an Elvis impersonator, so
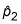
is 37 divided by 110 = 0.34.
The difference between these sample proportions (females – males) is 0.53 – 0.34 = 0.19.
Take 0.53 ∗ (1 – 0.53) to obtain 0.2941. Then divide that by 100 to get 0.0025. Then take 0.34 ∗ (1 – 0.34) to obtain 0.2244. Then divide that by 110 to get 0.0020. Add these two results to get 0.0025 + 0.0020 = 0.0045. Then find the square root of 0.0045 which is 0.0671.
1.96 ∗ 0.0671 gives you 0.13, or 13%, which is the margin of error.
Your 95% confidence interval for the difference between the percentage of females who have seen an Elvis impersonator and the percentage of males who have seen an Elvis impersonator is 0.19 or 19% (which you got in Step 3), plus or minus 13%. The lower end of the interval is 0.19 – 0.13 = 0.06 or 6%; the upper end is 0.19 + 0.13 = 0.32 or 32%.
To interpret these results within the context of the problem, you can say with 95% confidence that a higher percentage of females than males have seen an Elvis impersonator, and the difference in these percentages is somewhere between 6% and 32%, based on your sample.
The temptation is to say, “Well, I knew a greater proportion of women has seen an Elvis impersonator because that sample proportion was 0.53 and for men it was only 0.34. Why do I even need a confidence interval?” All those two numbers tell you is something about those 210 people sampled. You also need to factor in variation using the margin of error to be able to say something about the entire populations of men and women.
Of course, there are some guys out there that wouldn’t admit they’d ever seen an Elvis impersonator (although they’ve probably pretended to be one doing karaoke at some point). This may create some bias in the results.
Notice that you could get a negative value for
For example, if you had switched the males and females, you would have gotten –0.19 for this difference. That’s okay, but you can avoid negative differences in the sample proportions by having the group with the larger sample proportion serve as the first group (here, females).
However, even if the group with the larger sample proportion serves as the first group, sometimes you will still get negative values in the confidence interval. Suppose in the above example that only 0.43 of women had seen an Elvis impersonator. Thus, the difference in proportions is 0.09, and the upper end of the confidence interval is 0.09 + 0.13 = 0.22 while the lower end is 0.09 – 0.13 = –0.04. This means that the true difference is reasonably anywhere from 22% more women to 4% more men. It’s too close to tell for sure.





