Statistics For Dummies, 2nd Edition
Book image
Explore Book Buy On Amazon
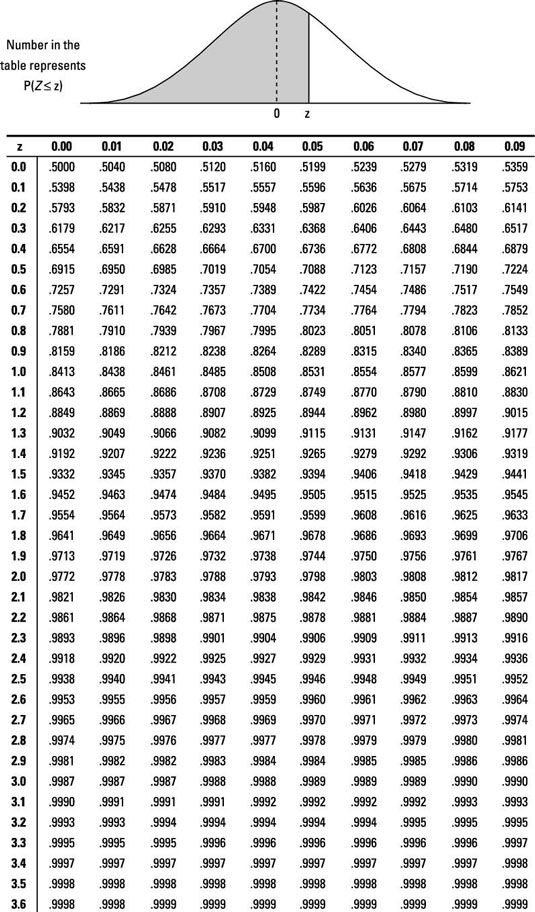
When you test a hypothesis about a population, you can use your test statistic to decide whether to reject the null hypothesis, H0. You make this decision by coming up with a number, called a p-value.

A p-value is a probability associated with your critical value. The critical value depends on the probability you are allowing for a Type I error. It measures the chance of getting results at least as strong as yours if the claim (H0) were true.

The following figure shows the locations of a test statistic and their corresponding conclusions.

Decisions for Ha: not-equal-to.
Note that if the alternative hypothesis is the less-than alternative, you reject H0 only if the test statistic falls in the left tail of the distribution (below –2). Similarly, if Ha is the greater-than alternative, you reject H0 only if the test statistic falls in the right tail (above 2).

To find the p-value for your test statistic:

  1. Look up your test statistic on the appropriate distribution — in this case, on the standard normal (Z-) distribution (see the following Z-tables).

    z-score table 1
    z-score table 2

  2. Find the probability that Z is beyond (more extreme than) your test statistic:

    1. If Ha contains a less-than alternative, find the probability that Z is less than your test statistic (that is, look up your test statistic on the Z-table and find its corresponding probability). This is the p-value. (Note: In this case, your test statistic is usually negative.)

    2. If Ha contains a greater-than alternative, find the probability that Z is greater than your test statistic (look up your test statistic on the Z-table, find its corresponding probability, and subtract it from one). The result is your p-value. (Note: In this case, your test statistic is usually positive.)

    3. If Ha contains a not-equal-to alternative, find the probability that Z is beyond your test statistic and double it. There are two cases:

      If your test statistic is negative, first find the probability that Z is less than your test statistic (look up your test statistic on the Z-table and find its corresponding probability). Then double this probability to get the p-value.

      If your test statistic is positive, first find the probability that Z is greater than your test statistic (look up your test statistic on the Z-table, find its corresponding probability, and subtract it from one). Then double this result to get the p-value.

Suppose you are testing a claim that the percentage of all women with varicose veins is 25%, and your sample of 100 women had 20% with varicose veins. Then the sample proportion p=0.20. The standard error for your sample percentage is the square root of p(1-p)/n which equals 0.04 or 4%. You find the test statistic by taking the proportion in the sample with varicose veins, 0.20, subtracting the claimed proportion of all women with varicose veins, 0.25, and then dividing the result by the standard error, 0.04. These calculations give you a test statistic (standard score) of –0.05 divided by 0.04 = –1.25. This tells you that your sample results and the population claim in H0 are 1.25 standard errors apart; in particular, your sample results are 1.25 standard errors below the claim.

When testing H0: p = 0.25 versus Ha: p < 0.25, you find that the p-value of -1.25 by finding the probability that Z is less than -1.25. When you look this number up on the above Z-table, you find a probability of 0.1056 of Z being less than this value.

Note: If you had been testing the two-sided alternative,

image3.png

the p-value would be 2 ∗ 0.1056, or 0.2112.

If the results are likely to have occurred under the claim, then you fail to reject H0 (like a jury decides not guilty). If the results are unlikely to have occurred under the claim, then you reject H0 (like a jury decides guilty).

About This Article

This article is from the book:

About the book author:

Deborah Rumsey, PhD, is an auxiliary faculty member and program specialist in department of statistics at The Ohio State University. An author of several Dummies books, she is a fellow of the American Statistical Association.

This article can be found in the category: