The practice questions here help you in determining appropriate sample sizes required to achieve a certain margin of error. Figure out the sample size needed in the following problems.
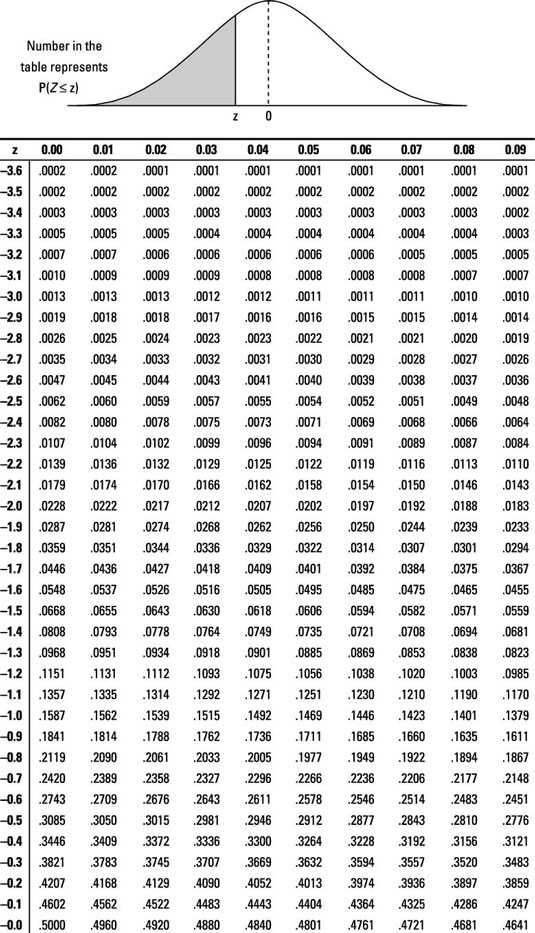
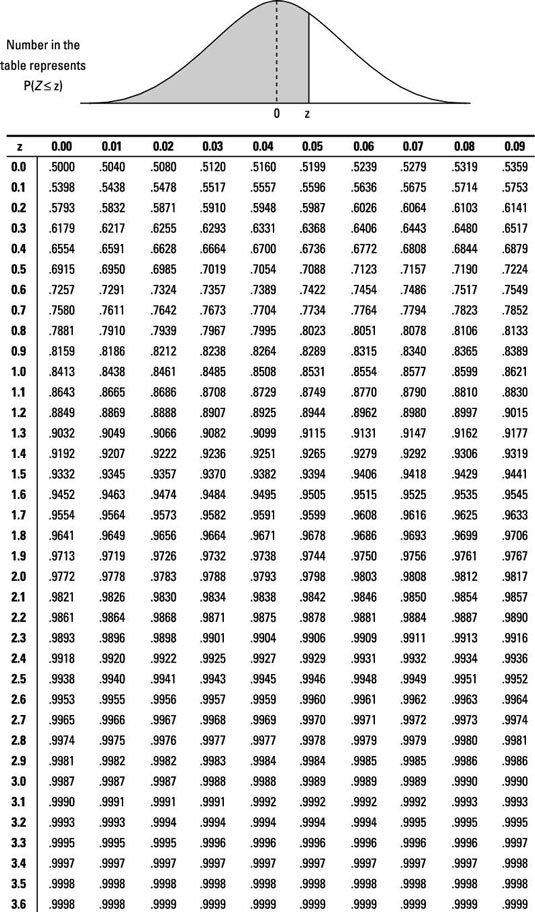
Sample questions
A physician wants to estimate the average BMI (body mass index, a measure that combines information about height and weight) for her adult patients.
She decides to draw a sample of clinical records and retrieve this information from them. She wants an estimate with a margin of error of 1.5 units of BMI, with 95% confidence, and believes that the national population standard deviation of adult BMI of 4.5 also applies to her patients. She knows that BMI is approximately normally distributed for adults. How large a sample does she need to draw?
Answer: The sample size must be at least 35 to produce a margin of error of plus/minus 1.5 units of BMI.
The formula to calculate the sample size needed for a confidence interval for a sample mean is

where n is the sample size required, z* is the value from the table for the chosen confidence level,

is the population standard deviation, and MOE is the margin of error. For this example, z* is 1.96,

is 1.6, and the MOE is 1.5.

Samples sizes are always rounded up to the nearest integer, so the sample size must be at least 35.
A physician wants to estimate the height of 6-year-old boys in her community, using a random sample drawn from administrative records.
She wants an estimate with a margin of error of 0.5 inches, with 95% confidence, and believes that the population standard deviation of 1.8 inches applies to her population. She also knows that height is approximately normally distributed for this population. How large a sample does she need to draw?
Answer: The sample size must be at least 50 to produce a margin of error of plus/minus 0.5 inches.
The formula to calculate sample size to estimate a mean, when the standard deviation is known, is

where n is the sample size required, z* is the value from the table for the chosen confidence level,

is the population standard deviation, and MOE is the margin of error. For this example, z* is 1.96,

is 1.6, and the MOE is 0.5.

She needs a sample of at least 50 to achieve the desired precision.
You want to estimate the average height of 10-year-old boys in your community.
The population standard deviation is 3 inches. What size sample do you need for a margin of error of no more than plus/minus 1 inch and a confidence level of 95% when constructing a confidence interval for the mean height of all 10-year-old boys?
Answer: The sample size must be at least 35 to produce a margin of error of plus/minus 1 inch.
The formula to find the required sample size based on a desired margin of error is

Here, MOE is the margin of error, z* is the z*-value corresponding to your desired confidence level, and

is the population standard deviation. If

is unknown, you can do a small pilot study to find the standard deviation of the sample (including making a conservative adjustment to the sample standard deviation to be safe).
Substitute the known values into the formula:

Always round up the answer to the nearest whole number to be sure the sample size is large enough to give the margin of error needed. So n greater than or equal to 35. That means that you need at least 35 boys in your sample to get a margin of error of no more than 1 inch for average height.
Note that a sample size of 35 will give you the margin of error you want; a higher sample size will give you an even lower margin of error.
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.





