In a system of inequalities, you see more than one inequality with more than one variable. Before pre-calculus, teachers tend to focus mostly on systems of linear inequalities. The graphs of those inequalities are straight lines with areas shaded on either side of the lines. In pre-calculus, though, you expand your study to systems of nonlinear inequalities because they are more thorough in the types of equations they cover (straight lines are so boring!).
In these systems of inequalities, at least one inequality isn’t linear. The only way to solve a system of inequalities is to graph the solution. You may be required to graph inequalities that you haven’t seen since pre-algebra. But for the most part, these inequalities probably resemble common parent functions and conic sections. The only difference between then and now is that the line that you graph is either solid or dashed, depending on the problem, and you get to color (or shade) where the solutions lie!
For example, consider the following nonlinear system of inequalities:
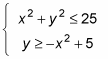
To solve this system of equations, first graph the system. The fact that these expressions are inequalities and not equations doesn’t change the general shape of the graph at all. Therefore, you can graph these inequalities just as you would graph them if they were equations. The top equation of this example is a circle. This circle is centered at the origin, and the radius is 5. The second equation is an upside-down parabola. It is shifted vertically 5 units and flipped upside down. Because both of the inequality signs in this example include the equality line underneath (the first one is “less than or equal to” and the second is “greater than or equal to”), both lines should be solid.
If the inequality symbol says “strictly greater than: >” or “strictly less than:
After graphing, pick one test point that isn’t on a boundary and plug it into the equations to see if you get true or false statements. The point that you pick as a solution must work in every equation.
For example, say your test point is (0, 4). If you plug this point into the inequality for the circle, you get
This statement is true because
so you shade inside the circle. Now plug the same point into the parabola to get
but because 4 isn’t greater than 5, this statement is false. You shade outside the parabola.
The solution of this system of inequalities is where the shading overlaps.
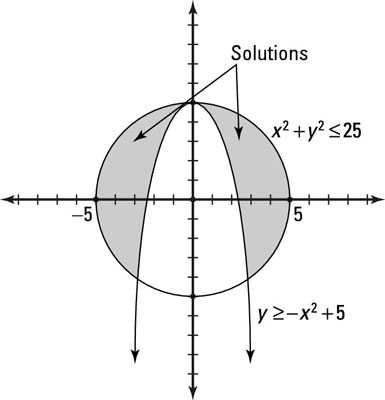
This figure shows the final graph.





