In pre-calculus, you use trig functions to solve algebraic equations. When you find the value of the angle in an equation, which is the angle that is a solution to the equation, you use that as the reference angle to find other angles on the unit circle that will also be solutions to the equation. Usually you can find two, but you may find none, one, or more than two.
You can use your knowledge of trig functions to make an educated guess about how many solutions an equation can have. If the sine or cosine values are greater than 1 or less than –1, for instance, the equation has no solutions.
Remember: Theta prime,
is the name given to the reference angle, and theta,
is the actual solution to the equation, so you can find solutions by using the following quadrant rules, as shown in the figure:
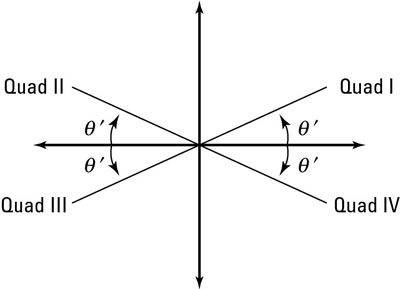

When you see a trig equation that asks you to solve for an unknown angle, you move backward from what you're given to arrive at a solution that makes sense. This solution should be in the form of an angle measurement, and the location of the angle should be in the correct quadrant. Knowledge of the unit circle comes in handy here because you'll be thinking of angles that fulfill the requirements of the given equation.
Suppose you're asked to solve 2 cos x = 1. To solve, you need to think about which angles on the unit circle have cosine values that equal 1 when multiplied by 2. Follow these steps:
Isolate the trig function on one side.
You solve for cos x by dividing both sides by 2: cos x = 1/2.
Determine which quadrants your solutions lie in.
Keeping in mind that cosine is an x value, you draw four triangles — one in each quadrant — with the x-axis legs labeled 1/2 or –1/2. The next figure shows these four triangles.
The two triangles on the left have a value of –1/2 for the horizontal leg, not 1/2. Therefore, you can eliminate them. Your solutions are in quadrants I and IV.
 These four triangles help you locate the solutions.
These four triangles help you locate the solutions.Fill in the missing leg values for each triangle.
You've already marked the x-axis legs. Based on knowledge of the unit circle and special triangles, you know that the side parallel to the y-axis has to be

and that the hypotenuse is 1. The next figure shows the two labeled triangles.
 The two solution triangles in the unit circle.
The two solution triangles in the unit circle.Determine the reference angle.
In the special right triangles, a side length of 1/2 is the short leg of a 30-60-90-degree right triangle. Therefore, the cosine (or the part along the x-axis) is the short leg and the vertical leg is the long leg. So the vertex of the angle at the center of the unit circle has a measure of 60 degrees, making the reference angle

Express the solutions in standard form.
The reference angle is

The first quadrant solution is the same as the reference angle:

The fourth quadrant solution is






