Pre-Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice)
Explore Book Buy On AmazonIn a nonlinear system, at least one equation has a graph that isn’t a straight line — that is, at least one of the equations has to be nonlinear. Your pre-calculus instructor will tell you that you can always write a linear equation in the form Ax + By = C (where A, B, and C are real numbers); a nonlinear system is represented by any other form. Examples of nonlinear equations include, but are not limited to, any conic section, polynomial of degree at least 2, rational function, exponential, or logarithm.
How to solve a nonlinear system when one equation in the system is nonlinear
If one equation in a system is nonlinear, you can use substitution. In this situation, you can solve for one variable in the linear equation and substitute this expression into the nonlinear equation, because solving for a variable in a linear equation is a piece of cake! And any time you can solve for one variable easily, you can substitute that expression into the other equation to solve for the other one.
For example, follow these steps to solve this system:
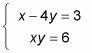
Solve the linear equation for one variable.
In this example, the top equation is linear. If you solve for x, you get x = 3 + 4y.
Substitute the value of the variable into the nonlinear equation.
When you plug 3 + 4y into the second equation for x, you get (3 + 4y)y = 6.
Solve the nonlinear equation for the variable.
When you distribute the y, you get 4y2 + 3y = 6. Because this equation is quadratic, you must get 0 on one side, so subtract the 6 from both sides to get 4y2 + 3y – 6 = 0. You have to use the quadratic formula to solve this equation for y:
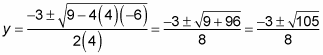
Substitute the solution(s) into either equation to solve for the other variable.
Because you found two solutions for y, you have to substitute them both to get two different coordinate pairs. Here’s what happens when you do:
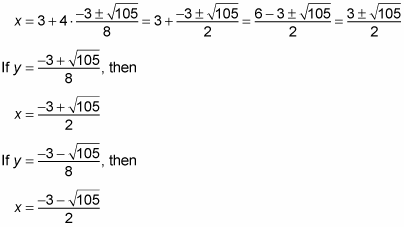
Therefore, you get the solutions to the system:
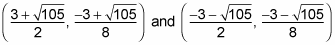
These solutions represent the intersection of the line x – 4y = 3 and the rational function xy = 6.
How to solve a nonlinear system when both system equations are nonlinear
If both of the equations in a system are nonlinear, well, you just have to get more creative to find the solutions. Unless one variable is raised to the same power in both equations, elimination is out of the question. Solving for one of the variables in either equation isn’t necessarily easy, but it can usually be done. After you solve for a variable, plug this expression into the other equation and solve for the other variable just as you did before. Unlike linear systems, many operations may be involved in the simplification or solving of these equations. Just remember to keep your order of operations in mind at each step of the way.
When both equations in a system are conic sections, you’ll never find more than four solutions (unless the two equations describe the same conic section, in which case the system has an infinite number of solutions — and therefore is a dependent system). Four is the limit because conic sections are all very smooth curves with no sharp corners or crazy bends, so two different conic sections can’t intersect more than four times.
For example, suppose a problem asks you to solve the following system:
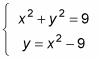
Doesn’t that problem just make your skin crawl? Don’t break out the calamine lotion just yet, though. Follow these steps to find the solutions:
Solve for x2 or y2 in one of the given equations.
The second equation is attractive because all you have to do is add 9 to both sides to get y + 9 = x2.
Substitute the value from Step 1 into the other equation.
You now have y + 9 + y2 = 9 — a quadratic equation.
Solve the quadratic equation.
Subtract 9 from both sides to get y + y2 = 0.
Remember that you’re not allowed, ever, to divide by a variable.
You must factor out the greatest common factor (GCF) instead to get y(1 + y) = 0. Use the zero product property to solve for y = 0 and y = –1.
Substitute the value(s) from Step 3 into either equation to solve for the other variable.
This example uses the equation solved for in Step 1. When y is 0, 9 = x2, so
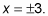
When y is –1, 8 = x2, so
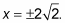
Be sure to keep track of which solution goes with which variable, because you have to express these solutions as points on a coordinate pair. Your answers are
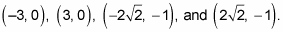
This solution set represents the intersections of the circle and the parabola given by the equations in the system.

