Oftentimes, your math teachers will ask you to prove equalities that involve the secant, cosecant, or cotangent functions. Whenever you see these functions in a proof, the reciprocal identities usually are the best places to start. Without the reciprocal identities, you can go in circles all day without ever actually getting anywhere.
For example, to prove
you can work with the left side of the equality only. Follow these simple steps:
Convert all functions to sines and cosines.
The left side of the equation now looks like this:
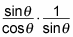
Cancel all possible terms.
Canceling gives you
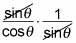
which simplifies to
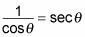
You can't leave the reciprocal function in the equality, so convert back again.


