How to Graph a Secant Function

You can graph a secant function f(x) = sec x by using steps similar to those for tangent and cotangent. As with tangent and cotangent, the graph of secant has asymptotes. This is because secant is defined as

The cosine graph crosses the x-axis on the interval

at two places, so the secant graph has two asymptotes, which divide the period interval into three smaller sections. The parent secant graph doesn't have any x-intercepts (finding them on any transformed graph is hard, so usually you won't be asked to).

Follow these steps to picture the parent graph of secant:

1. Find the asymptotes of the secant graph.

   Because secant is the reciprocal of cosine, any place on the cosine graph where the value is 0 creates an asymptote on the secant graph (because any fraction with 0 in the denominator is undefined). Finding these points first helps you define the rest of the graph.

   The parent graph of cosine has values of 0 at angles

   

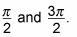
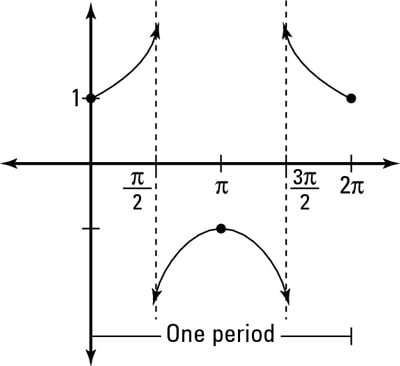
   So the graph of secant has asymptotes at those same values. The figure shows only the asymptotes.

   

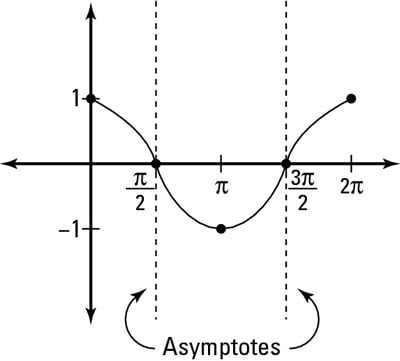   The graph of cosine reveals the asymptotes of secant.

2. Calculate what happens to the graph at the first interval between the asymptotes.

   The period of the parent cosine graph starts at 0 and ends at

   

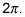
   You need to figure out what the graph does in between the following points:

   • Zero and the first asymptote at

     

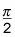
   • The two asymptotes in the middle

   • The second asymptote and the end of the graph at

     

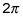
   Start on the interval

   

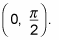
   The graph of cosine goes from 1, into fractions, and all the way down to 0. Secant takes the reciprocal of all these values and ends on this first interval at the asymptote. The graph gets bigger and bigger rather than smaller, because as the fractions in the cosine function get smaller, their reciprocals in the secant function get bigger.

3. Repeat Step 2 for the second interval

   

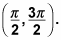
   Going from pi backward to pi/2,the graph of cosine goes from –1, into negative fractions, and all the way down to 0. Secant takes the reciprocal of all these values and ends on this interval at the asymptote. The graph gets bigger rather than smaller in the negative direction because, as the fractions in the cosine function get smaller (closer to zero), their reciprocals in the secant function get bigger in the negative direction.

   Likewise, going from pi to 3pi/2, the graph of cosine goes from –1, into negative fractions, and all the way down to 0. Secant takes the reciprocal of all these values and ends on this interval at the asymptote. The graph gets bigger in the negative direction, rather than smaller, because as the fractions in the cosine function get smaller (closer to zero), their reciprocals in the secant function get bigger in the negative direction.

4. Repeat Step 2 for the last interval

   

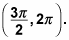
   This interval is a mirror image of what happens in the first interval.

5. Find the domain and range of the graph.

   

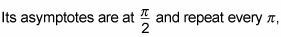
   so the domain of secant, where n is an integer, is

   

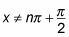
   The graph exists only for numbers

   

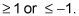
   Its range, therefore, is

   

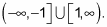
   You can see the parent graph of

   

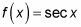
   in the figure.