![]()
combinations formula. If the exponent is relatively small, you can use a shortcut called Pascal's triangle to find these coefficients. If not, you can always rely on algebra!
Pascal's triangle, named after the famous mathematician Blaise Pascal, names the binomial coefficients for the binomial expansion. It is especially useful when raising a binomial to lower degrees.
For example, if a sadistic teacher asked you to find (3x + 4)10, you probably wouldn't want to use Pascal's triangle; instead, you'd just use the algebraic formula described shortly. The figure illustrates this concept. The top number of the triangle is 1, as well as all the numbers on the outer sides. To get any term in the triangle, you find the sum of the two numbers above it.
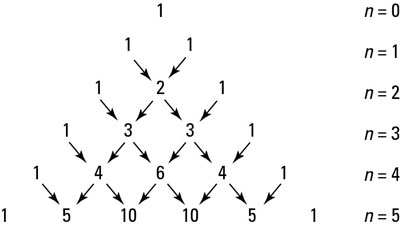 Determining coefficients with Pascal's triangle
Determining coefficients with Pascal's triangleIf you need to find the coefficients of binomials algebraically, there is a formula for that as well. The rth coefficient for the nth binomial expansion is written in the following form:
![]()
You may recall the term factorial from your earlier math classes. If not, here is a reminder: n!, which reads as "n factorial," is defined as
![]()
You read the expression for the binomial coefficient
![]()
as "n choose r." You usually can find a button for combinations on a calculator. If not, you can use the factorial button and do each part separately.
To make things a little easier, 0! is defined as 1. Therefore, you have these equalities:

For example, to find the binomial coefficient given by
![]()
substitute the values into the formula:
![]()






