How to Combine Various Transformations

Certain mathematical expressions allow you to combine stretching, shrinking, translating, and reflecting a function all into one graph. An expression that shows all the transformations in one is

where

• a is the vertical transformation.

• c is the horizontal transformation.

• h is the horizontal shift.

• v is the vertical shift.

For instance, f(x) = –2(x – 1)² + 4 moves the graph of y = x² right 1 unit, vertically stretches it by a factor of 2, reflects it upside down, and then moves it up 4 units.

This figure shows each stage.

• Figure a is the parent graph: k(x) = x².

• Figure b is the horizontal shift to the right by one: h(x) = (x – 1)².

• Figure c is the vertical stretch of two: f(x) = –2(x – 1)². (Notice that because the value was negative, the graph was also turned upside down.)

• Figure d is the vertical shift up by four: g(x) = –2(x – 1)² + 4.

The following transformation illustrates the importance of the order of the process. You graph the function

with the following steps:

1. Rewrite the function in the form

   

   Reorder the function so that the x comes first (in descending order). And don’t forget the negative sign! Here it is:

   

2. Factor out the coefficient in front of the x.

   You now have

   

3. Reflect the parent graph.

   Because the –1 is inside the square-root function, q(x) is a horizontal reflection over a vertical line of

   

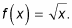
4. Shift the graph.

   The factored form of q(x) (from Step 2) reveals that the horizontal shift is four to the right.

   

This figure shows the graph of