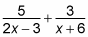When your pre-calculus instructor asks you to decompose partial fractions, it's actually not as messy as it sounds. The process of decomposing a partial fraction requires you to separate the fraction into two (or sometimes more) disjointed fractions with variables (usually A, B, C, and so on) standing in as placeholders in the numerator. Then you can set up a system of equations to solve for these variables.
The process of partial fractions takes one fraction and expresses it as the sum or difference of two or more other fractions. There are many reasons why you'd need to do this. In calculus, this process is useful before you integrate a function. Because integration is so much easier when the degree of a rational function is 1 in the denominator, partial fraction decomposition is a useful tool for you.
Now try an example. Say you need to write the partial fraction decomposition of the following fraction:
To do this, you would follow these steps:
Factor the denominator and rewrite it as A over one factor and B over the other.
You do this because you want to break the fraction into two. The process unfolds as follows:
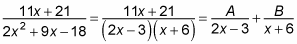
Multiply every term you've created by the factored denominator and then cancel.
You'll multiply a total of three times in this example:
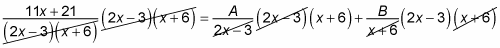
This expression equals the following:
11x + 21 = A(x + 6) + B(2x – 3)
Distribute A and B.
This step gives you
11x + 21 = Ax + 6A + 2Bx – 3B
On the right side of the equation only, put all terms with an x together and all terms without it together.
Rearranging gives you
11x + 21 = Ax + 2Bx + 6A – 3B
Factor out the x from the terms on the right side.
You now have
11x + 21 = (A + 2B)x + 6A – 3B
Create a system out of this equation by pairing up terms.
For an equation to work, everything must be in balance. Because of this fact, the coefficients of x must be equal and the constants must be equal. If the coefficient of x is 11 on the left and A + 2B on the right, you can say that 11 = A + 2B is one equation. Constants are the terms with no variable, and in this case, the constant on the left is 21. On the right side, 6A – 3B is the constant (because no variable is attached) and so 21 = 6A – 3B.
Solve the system, using either substitution or elimination.
In this example, you'll use elimination. You have the following equations:
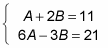
So you can multiply the top equation by –6 and then add to eliminate and solve. You find that A = 5 and B = 3.
Write the solution as the sum of two fractions.