You can use two equidistant points to determine the perpendicular bisector of a segment. (To “determine” something means to fix or lock in its position, basically to show you where something is.) Here’s the theorem.
Two equidistant points determine the perpendicular bisector: If two points are each (one at a time) equidistant from the endpoints of a segment, then those points determine the perpendicular bisector of the segment. (Here’s an easy way to think about it: If you have two pairs of congruent segments, then there’s a perpendicular bisector.)

This theorem is a royal mouthful, so the best way to understand it is visually. Consider the kite-shaped diagram in the above figure.
The theorem works like this: If you have one point (like X) that’s equally distant from the endpoints of a segment (W and Y) and another point (like Z) that’s also equally distant from the endpoints, then the two points (X and Z) determine the perpendicular bisector (line XZ) of that segment (segment WY).

Here’s a “SHORT” proof that shows how to use this equidistance theorem as a shortcut so you can skip showing that triangles are congruent.
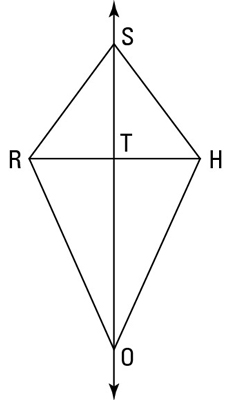
You can do this proof using congruent triangles, but it’d take you about nine steps and you’d have to use two different pairs of congruent triangles.
Statement 1:
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: If angles, then sides.
Statement 3:
Reason for statement 3: Given.
Statement 4:
Reason for statement 4: If two points (S and O) are each equidistant from the endpoints of a segment (segment RH), then they determine the perpendicular bisector of that segment.
Statement 5:
Reason for statement 5: Definition of bisect.
Statement 6:
Reason for statement 6: Definition of midpoint.

