You can use the following four-step solution method to solve a 2-D problem.
Start with a problem: What's the locus of all points 3 units from a given circle whose radius is 10 units?
- Identify a pattern.
This is likely a problem in which you can immediately picture a pattern without going through the one-point-at-a-time routine. When you read that you want all points that are 3 units from a circle, you can see that a bigger circle will do the trick.
Points 3 units away from the original circle that form another circle.This figure shows the given circle of radius 10 and the circle of radius 13 that you'd draw for your solution.
- Look outside the pattern for points to add.
Do you see what Step 1 leaves out? Right—it's a smaller circle with a radius of 7 inside the original circle.
Points 3 units away from the original circle that form a smaller circle."Missing" this second circle may seem a bit contrived, and granted, many people immediately see that the solution should include both circles. However, people often do focus on one particular pattern (the biggest circle in this problem) to the exclusion of everything else. Their minds sort of get in a rut, and they have trouble seeing anything other than the first pattern or idea that they latch onto. And that's why it's so important to explicitly go through this second step of the four-step method.
- Look inside the pattern for points to exclude. All points of the 7-unit-radius and 13-unit-radius circles satisfy the given condition, so no points need to be excluded.
- Draw the locus and describe it in words. The final figure shows the locus, and the caption gives its description.
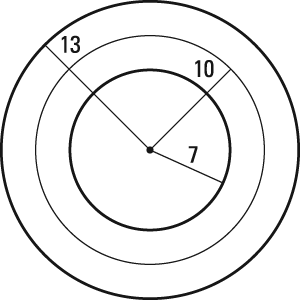The locus of points 3 units from the given circle is two circles concentric with the original circle with radii of 7 and 13 units.Like a walk in the park, right?
