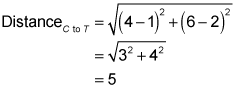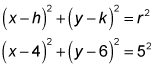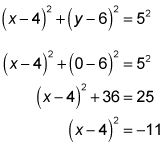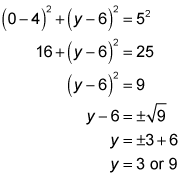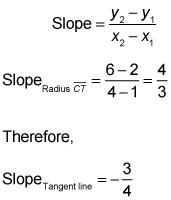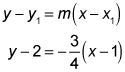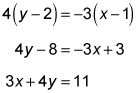How to Use Circle Equations in Coordinate Geometry

You can apply equations and algebra (that is, use analytic methods) to circles that are positioned in the x-y coordinate system. For example, there's a nice analytic connection between the circle equation and the distance formula because every point on a circle is the same distance from its center.

Here are the circle equations:

• Circle centered at the origin, (0, 0), x² + y² = r² where r is the circle's radius.
• Circle centered at any point (h, k), (x – h)² + (y – k)² = r² where (h, k) is the center of the circle and r is its radius. (As you may recall from an algebra course, it seems backward, but subtracting any positive number h from x actually moves the circle to the right, and subtracting any positive number k from y moves the circle up; adding a number to x moves the circle left, and adding a positive number to y moves the circle down.)

Now, try a circle problem:

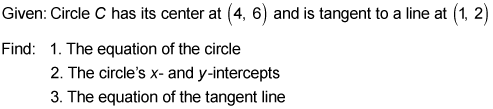
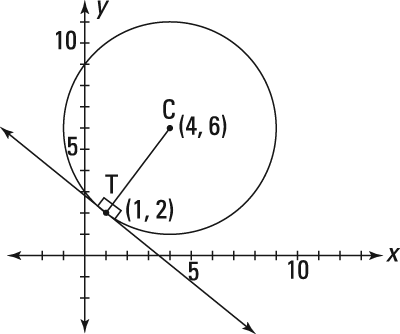
Here is the proof diagram.

1. Find the equation of the circle. All you need for the equation of a circle is its center (you know it) and its radius. The radius of the circle is just the distance from its center to any point on the circle. Since the point of tangency is given, that's the point to use. To wit —

   

   Now you finish by plugging the center coordinates and the radius into the general circle equation:

   

2. Find the circle's x- and y-intercepts. To find the x-intercepts for any equation, you just plug in 0 for y and solve for x:

   

   You can't square something and get a negative number, so this equation has no solution; therefore, the circle has no x-intercepts. (Of course, you can just look at the figure and see that the circle doesn't intersect the x-axis, but it's good to know how the math confirms this.) To find the y-intercepts, plug in 0 for x and solve for y :

   

   Thus, the circle's y-intercepts are (0, 3) and (0, 9).

3. Find the equation of the tangent line. For the equation of a line, you need a point (you have it) and the line's slope. A tangent line is perpendicular to a radius drawn to the point of tangency. So just compute the slope of the radius, and then the opposite reciprocal of that is the slope of the tangent line:

   

   Now you plug this slope and the coordinates of the point of tangency into the point-slope form for the equation of a line:

   

   Now clean this up a bit:

   

Of course, if you instead choose to put this in slope-intercept form, you get

Over and out.