You can use the Secant-Secant Power Theorem to solve some circle problems. This theorem involves — are you sitting down — two secants! (If you’re trying to come up with a creative name for your child like Dweezil or Moon Unit, talk to Frank Zappa, not the guy who named the power theorems.)
Secant-Secant Power Theorem: If two secants are drawn from an external point to a circle, then the product of the measures of one secant’s external part and that entire secant is equal to the product of the measures of the other secant’s external part and that entire secant. (Whew!)
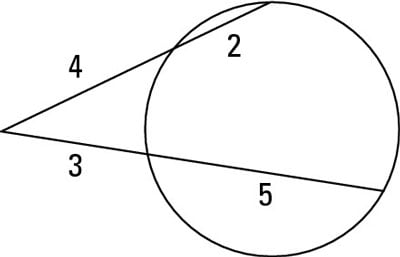
For instance, in the above figure,
4(4 + 2) = 3(3 + 5)
The following problem uses two power theorems:
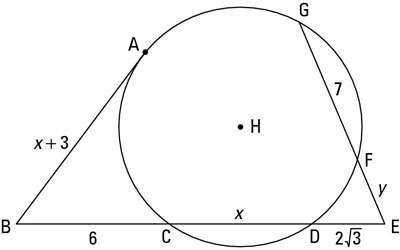
Given: Diagram as shown
Segment BA is tangent to circle H at A
Find: x and y
The figure includes a tangent and some secants, so look to your Tangent-Secant and Secant-Secant Power Theorems.

Now use the Secant-Secant Power Theorem with secants segment EC and segment EG to solve for y:
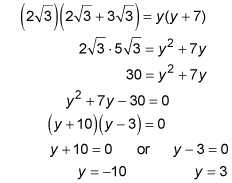
A segment can’t have a negative length, so y = 3. That does it.

