A circle is 360° all the way around; therefore, if you divide an arc’s degree measure by 360°, you find the fraction of the circle’s circumference that the arc makes up. Then, if you multiply the length all the way around the circle (the circle’s circumference) by that fraction, you get the length along the arc. So finally, here’s the formula you’ve been waiting for.
Arc length:

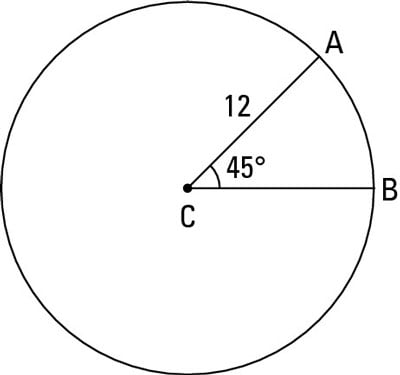
Its degree measure is 45° and the radius of the circle is 12, so here’s the math for its length:

Pretty simple, eh?

