One way to find the area of a regular hexagon is by first dividing it into equilateral triangles. You also need to use an apothem — a segment that joins a regular polygon’s center to the midpoint of any side and that is perpendicular to that side.
You’ll see what all this means when you solve the following problem:
First, sketch the hexagon with its three diagonals, creating six equilateral triangles. Then draw in an apothem, which goes from the center to the midpoint of a side. The following figure shows hexagon EXAGON with its diagonals and an apothem.
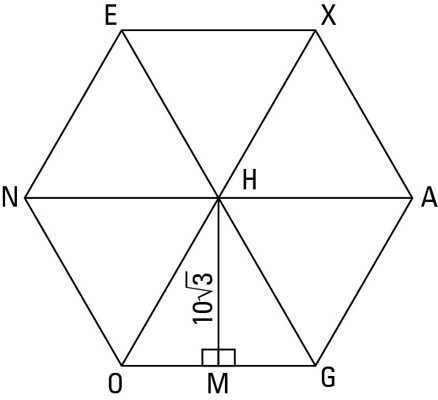

Now you can finish with either the regular polygon formula or the equilateral triangle formula (multiplied by 6). They’re equally easy. Take your pick. Here’s what it looks like with the regular polygon formula:
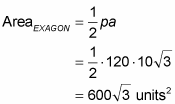
And here’s how to do it with the handy equilateral triangle formula:

For hexagon problems, 30°- 60°- 90° triangles and equilateral triangles often come in handy. A regular hexagon can be cut into six equilateral triangles, and an equilateral triangle can be divided into two 30°- 60°- 90° triangles. So if you’re doing a hexagon problem, you may want to cut up the figure and use equilateral triangles or 30°- 60°- 90° triangles to help you find the apothem, perimeter, or area.





