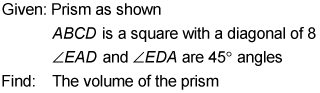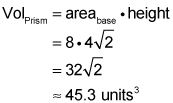The volume of a prism is given by the following formula:
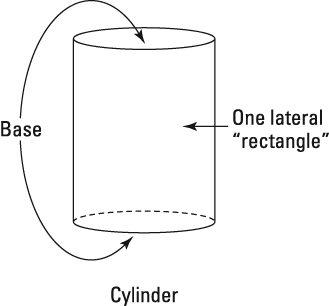
An ordinary box is a special case of a prism, so you can use this volume formula for a box, but you probably already know the easier way to compute a box's volume:
(Because the length times the width gives you the area of the base, these two methods really amount to the same thing.) To get the volume of a cube, the simplest type of box, you just take the length of one of its edges and raise it to the third power
Now, take a look at the formula in action.
Here's the diagram.
To use the volume formula, you need the prism's height (line CD) and the area of its base (triangle AED). (You've probably noticed that this prism is lying on its side. That's why its height isn't vertical and its base isn't on the bottom.)
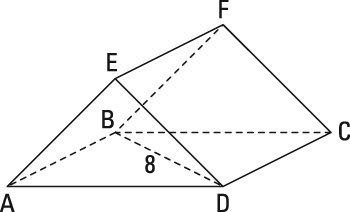
Get the height first. ABCD is a square, so triangle BCD (half of the square) is a 45°-45°-90° triangle with a hypotenuse of 8. To get the leg of a 45°-45°-90° triangle, you divide the hypotenuse by the square root of 2 (or use the Pythagorean Theorem, noting that a = b in this case). So that gives you
for the length of line CD, which, again, is the height of the prism.
And here's how you get the area of triangle AED. First, note that AD, like CD, is
Next, because angles EAD and EDA are given 45-degree angles, angle AED must be 90 degrees; thus, triangle AED is another 45°-45°-90° triangle.
The area of a right triangle is given by half the product of its legs (because you can use one leg for the triangle's base and the other for its height), so
You're all set to finish with the volume formula: