When you cross two lines with a third line, the third line is called a transversal. You can use the transversal theorems to prove that angles are congruent or supplementary.
Here’s a problem that lets you take a look at some of the theorems in action: Given that lines m and n are parallel, find the measure of angle 1.
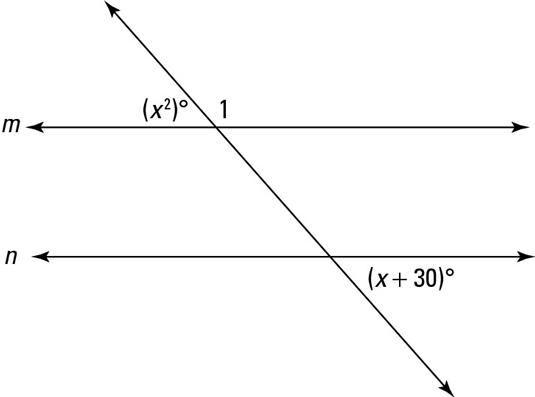
Here’s the solution:
(Or you can also say that because you’ve got the parallel-lines-plus-transversal diagram and two angles that are both obviously acute, they must be congruent.) Set them equal to each other and solve for x:
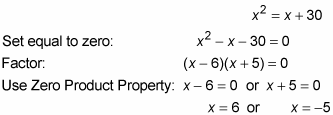
This equation has two solutions, so take them one at a time and plug them into the x’s in the alternate exterior angles.
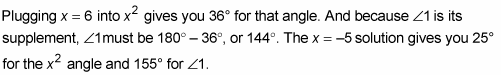
So 144° and 155° are your possible answers for angle 1.
When you get two solutions (such as x = 6 and x = –5) in a problem like this, you do not plug one of them into one of the x’s
and the other solution into the other x (like –5 + 30 = 25). You have to plug one of the solutions into all x’s, giving you one result for both angles
then you have to separately plug the other solution into all x’s, giving you a second result for both angles
Angles and segments can’t have negative measures or lengths. Make sure that each solution for x produces positive answers for all the angles or segments in a problem.
If a solution makes any angle or segment in the diagram negative, it must be rejected even if the angles or segments you care about end up being positive. However, do not reject a solution just because x is negative: x can be negative as long as the angles and segments are positive (x = –5, for example, works just fine in this problem).
Now here’s a proof that uses some of the transversal theorems:

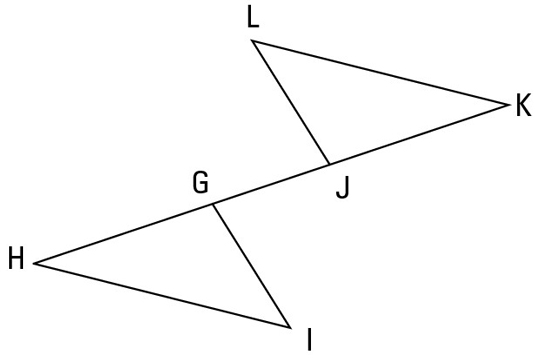
Check out the formal proof:
Statement 1:
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: Given.
Statement 3:
Reason for statement 3: If lines are parallel, then alternate interior angles are congruent.
Statement 4:
Reason for statement 4: Given.
Statement 5:
Reason for statement 5: If a segment (segment GJ) is subtracted from two congruent segments, then the differences are congruent.
Statement 6:
Reason for statement 6: SAS (using lines 1, 3, and 5).
Statement 7:
Reason for statement 7: CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
Statement 8:
Reason for statement 8: If alternate exterior angles are congruent, then lines are parallel.
Extend the lines in transversal problems. Extending the parallel lines and transversals may help you see how the angles are related.
For instance, if you have a hard time seeing that angle K and angle H are indeed alternate interior angles (for step 3 of the proof),
After doing that, you’re looking at the familiar parallel-line scheme shown in the following figure.
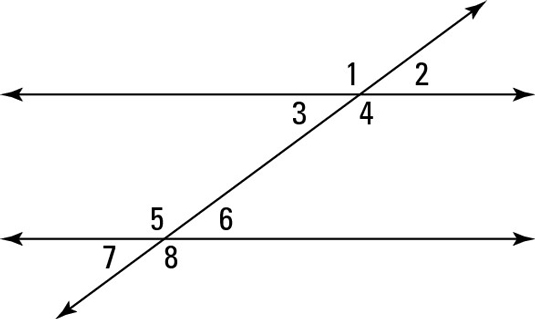
You can do the same thing for angle LJK and angle IGH by extending





