The Riemann Sum formula provides a precise definition of the definite integral as the limit of an infinite series. The Riemann Sum formula is as follows:
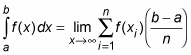
Below are the steps for approximating an integral using six rectangles:
Increase the number of rectangles (n) to create a better approximation:

Simplify this formula by factoring out w from each term:

Use the summation symbol to make this formula even more compact:

The value w is the width of each rectangle:

Each h value is the height of a different rectangle:

So here is the Riemann Sum formula for approximating an integral using n rectangles:

For a better approximation, use the limit

to allow the number of rectangles to approach infinity:






