You don’t need the mean value theorem for much, but it’s a famous theorem — one of the two or three most important in all of calculus — so you really should learn it. Fortunately, it’s very simple.
Here’s the formal definition of the theorem.
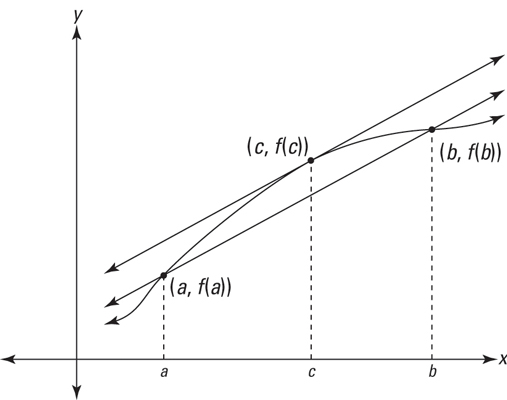
The mean value theorem: If f is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists a number c in (a, b) such that
Now for the plain English version. First you need to take care of the fine print. The requirements in the theorem that the function be continuous and differentiable just guarantee that the function is a regular, smooth function without gaps or sharp corners or cusps. But because only a few weird functions have gaps or pointy turns, you don’t often have to worry about these fine points.
Okay, so here’s what the theorem means. The secant line connecting points (a, f(a)) and (b, f(b)) in the figure has a slope given by the formula:
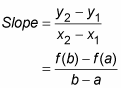
Note that this is the same as the right side of the equation in the mean value theorem. The derivative at a point is the same thing as the slope of the tangent line at that point, so the theorem just says that there must be at least one point between a and b where the slope of the tangent line is the same as the slope of the secant line from a to b.
Why must this be so? Here’s a visual argument. Imagine that you grab the secant line connecting (a, f (a)) and (b, f (b)), and then you slide it up, keeping it parallel to the original secant line. Can you see that the two points of intersection between this sliding line and the function — the two points that begin at (a, f (a)) and (b, f (b)) — will gradually get closer and closer to each other until they come together at (c, f (c))?
If you raise the line any further, you break away from the function entirely. At this last point of intersection, (c, f (c)), the sliding line touches the function at a single point and is thus tangent to the function there, while having the same slope as the original secant line.
Here’s a completely different sort of argument that should appeal to your common sense. If the function in the figure gives your car’s odometer reading as a function of time, then the slope of the secant line from a to b gives your average speed during that interval of time, because dividing the distance traveled, f (b) – f (a), by the elapsed time, b – a, gives you the average speed. The point (c, f (c)), guaranteed by the mean value theorem, is a point where your instantaneous speed — given by the derivative f´(c) — equals your average speed.
Now, imagine that you take a drive and average 50 miles per hour. The mean value theorem guarantees that you are going exactly 50 mph for at least one moment during your drive. Think about it. Your average speed can’t be 50 mph if you go slower than 50 the whole way or if you go faster than 50 the whole way. So, to average 50 mph, either you go exactly 50 for the whole drive, or you have to go slower than 50 for part of the drive and faster than 50 at other times. And if you’re going less than 50 at one point and more than 50 at a later point (or vice versa), you have to hit exactly 50 at least once as you speed up (or slow down). You can’t jump over 50 — like you’re going 49 one moment then 51 the next — because speeds go up by sliding up the scale, not jumping. So, at some point, your speedometer slides past 50 mph, and for at least one instant, you’re going exactly 50 mph. That’s all the mean value theorem says.

