Limits and Continuity in Calculus — Practice Questions

When you work with limit and continuity problems in calculus, there are a couple of formal definitions you need to know about. So, before you take on the following practice problems, you should first re-familiarize yourself with these definitions.

Here is the formal, three-part definition of a limit:

For a function f (x) and a real number a,

exists if and only if

(Note that this definition does not apply to limits as x approaches infinity or negative infinity.)

Now, here's the definition of continuity:

A function f (x) is continuous at a point a if three conditions are satisfied:

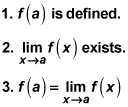
Now it's time for some practice problems.

Practice questions

Using the definitions and this figure, answer the following questions.

A function with many discontinuities.

1. At which of the following x values are all three requirements for the existence of a limit satisfied, and what is the limit at those x values?

   x = –2, 0, 2, 4, 5, 6, 8, 10, and 11.

2. At which of the x values are all three requirements for continuity satisfied?

Answers and explanations

1. All three requirements for the existence of a limit are satisfied at the x values 0, 4, 8, and 10:

   At 0, the limit is 2.

   At 4, the limit is 5.

   At 8, the limit is 3.

   At 10, the limit is 5.

   To make a long story short, a limit exists at a particular x value of a curve when the curve is heading toward some particular y value and keeps heading toward that y value as you continue to zoom in on the curve at the x value. The curve must head toward that y value (that height) as you move along the curve both from the right and from the left (unless the limit is one where x approaches infinity).

   The phrase heading toward is emphasized here because what happens precisely at the given x value isn't relevant to this limit inquiry. That's why there is a limit at a hole like the ones at x = 8 and x = 10.

2. The function in the figure is continuous at 0 and 4.

   The common-sense way of thinking about continuity is that a curve is continuous wherever you can draw the curve without taking your pen off the paper. It should be obvious that that's true at 0 and 4, but not at any of the other listed x values.