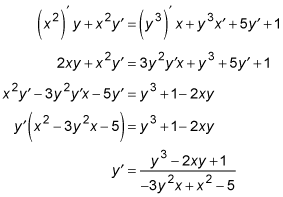Implicit differentiation problems are chain rule problems in disguise. Here's why: You know that the derivative of sin x is cos x, and that according to the chain rule, the derivative of sin (x3) is
You could finish that problem by doing the derivative of x3, but there is a reason for you to leave the problem unfinished here.
To do implicit differentiation, all you do (sort of) is every time you see a "y" in a problem, you treat it like the x3 is treated here. Thus, because the derivative of sin (x3) is
the derivative of sin y is
Then, after doing the differentiation,
By the way, "y" is used in the preceding explanation, but that's not the whole story. Consider that
is the same as
It's the variable on the top that you apply implicit differentiation to. This is typically y, but it could be any other variable. And it's the variable on the bottom that you treat the ordinary way. This is typically x, but it could also be any other variable.
Okay, time for a few practice questions.
Practice questions
if y3 – x2 = x + y, find

For x2y = y3x + 5y + x, find

Answers and explanations
By implicit differentiation,
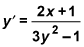
Start by taking the derivative of all four terms, using the chain rule (sort of) for all terms containing a y.
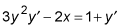
Then move all terms containing
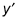
to the left, move all other terms to the right, and factor out
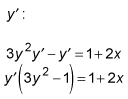
Divide and voilà!
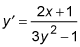
By implicit differentiation,
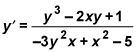
This time you have two products to deal with, so use the product rule for the two products and the regular rules for the other two terms.