You solve improper integrals by turning them into limit problems. You can’t just do them the regular way. Here’s how you solve improper integrals for functions that have vertical asymptotes. There are two cases: a vertical asymptote can be at the edge of the area in question or in the middle of it.
Case I: The function has a vertical asymptote at one of the limits of integration
What’s the area under
from 0 to 1? This function is undefined at x = 0, and it has a vertical asymptote there. So you’ve got to turn the definite integral into a limit:

This area is infinite, which probably doesn’t surprise you because the curve goes up to infinity. But hold on to your hat, despite the fact that the next function also goes up to infinity at x = 0, its area is finite!
Find the area under
from 0 to 1. This function is also undefined at x = 0, so the process is the same as in the previous example.
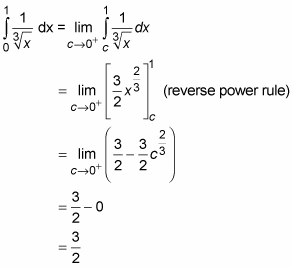
Convergence and Divergence: You say that an improper integral converges if the limit exists, that is, if the limit equals a finite number like in the second example. Otherwise, an improper integral is said to diverge — like in the first example.
Case II: The function has a vertical asymptote between the limits of integration
If the undefined point of the integrand is somewhere in between the limits of integration, you split the integral in two — at the undefined point — then turn each integral into a limit and go from there.
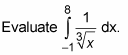
This integrand is undefined at x = 0.
Split the integral in two at the undefined point.

Turn each integral into a limit and evaluate.

Keep in mind that if you fail to notice that an integral has an undefined point between the limits of integration, and you integrate the ordinary way, you may get the wrong answer. The above problem,
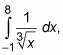
happens to work out right if you do it the ordinary way. However, if you do
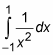
the ordinary way, not only do you get the wrong answer, you get the totally absurd answer of negative 2, despite the fact that the function is positive from –1 to 1. The moral: Don’t risk it.
If either part of the split up integral diverges, the original integral diverges. You can’t get, say, negative infinity for one part and infinity for the other part and add them up to get zero.





